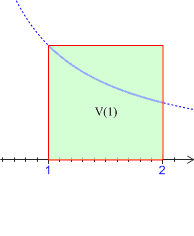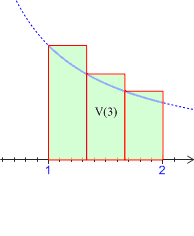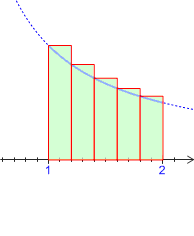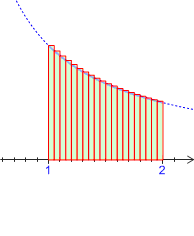
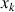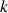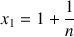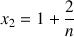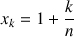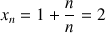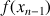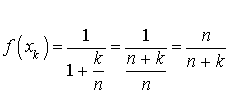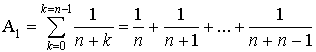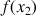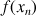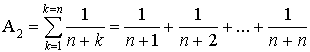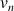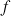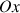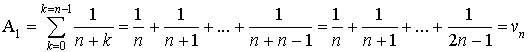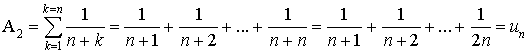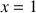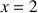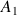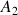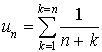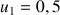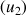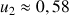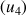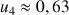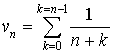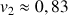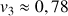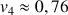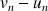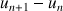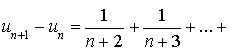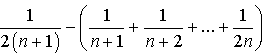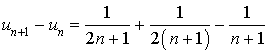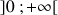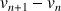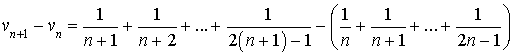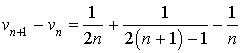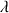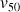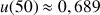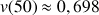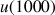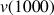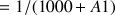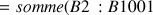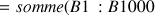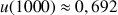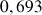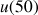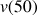Approximation d'une aire par deux suites adjacentes
Introduction
Prérequis :
Le logarithme népérien
Le calcul intégral
Durée : 60 minutes
Niveau : difficile
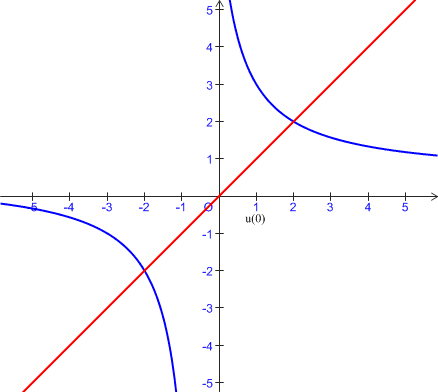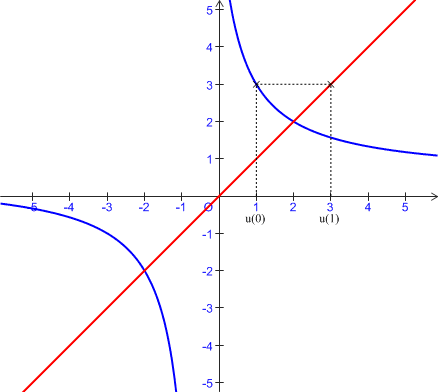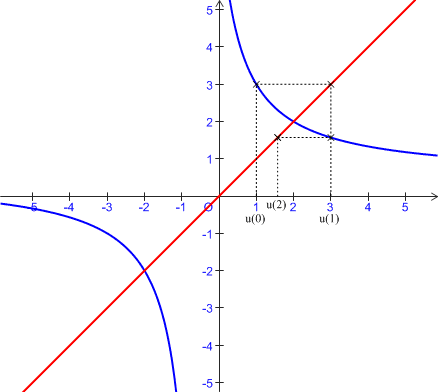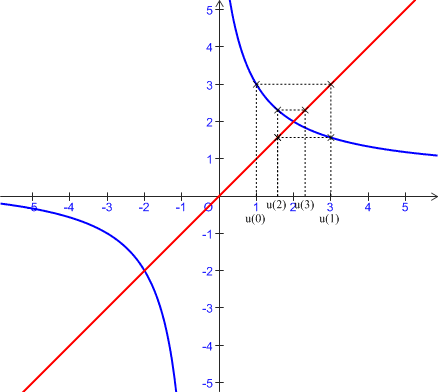
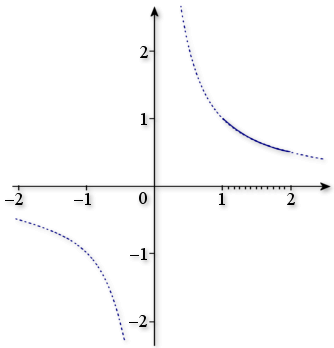
On considère la courbe
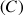de la fonction inverse : 
, pour
.
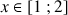On découpe l'intervalle
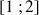en
intervalles de même amplitude dont les bornes sont notées
,
,...,
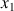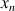avec
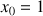et
.
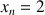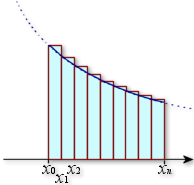
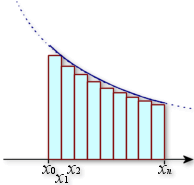
1) En considérant les aires des
rectangles dont l'un des sommets est sur la courbe
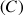, déterminer en fonction de
l'expression de l'aire coloriée sur chacun des dessins ci-dessous.
2) On considère :
la suite
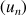définie par 
et la suite
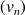définie par 
.
Montrer que 
.
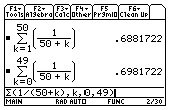
3) Déterminer
;
;
;
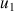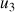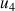et en donner des valeurs décimales approchées à
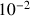près par défaut. Déterminer
;
;
;
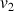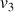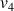et en donner des valeurs décimales approchées à
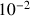près par excès.
4) Démontrer que les suites
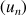et
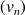sont adjacentes.
6) En utilisant un tableur (ou une calculatrice), donner une valeur approchée à
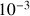près de
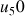et
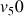puis de
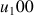et
.
