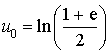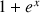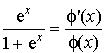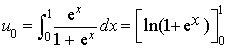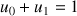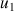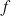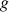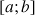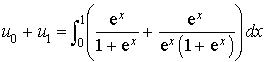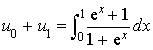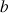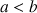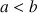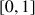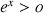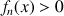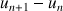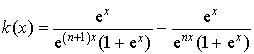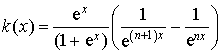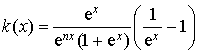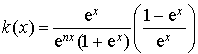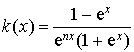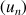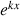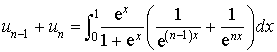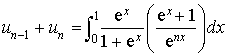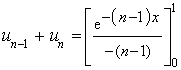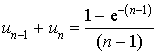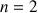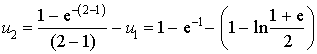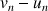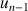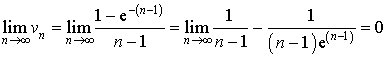Une suite définie par une intégrale
Introduction
Durée : 60 minutes
Niveau : moyen
Pour tout entier naturel
on considère la fonction
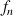définie sur R par :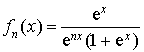 
L'objet de l'exercice est l'étude de la suite
définie pour tout entier naturel
par 
.
4) Donner le sens de variation de la suite
.
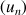5) Montrer que, pour tout entier
supérieur ou égal à 2, on a :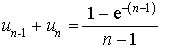 
.
Calculer
.
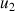6) Soit
la suite définie pour tout entier
supérieur ou égal à 2 par 
.
a. Calculer la limite de
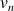quand
tend vers
.
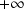b. Montrer que, pour tout entier
supérieur ou égal à 2, on a 
.
c. En déduire la limite de
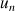quand
tend vers
.
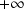