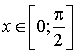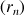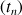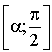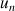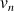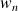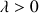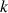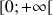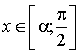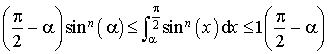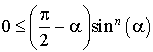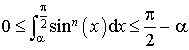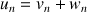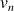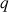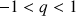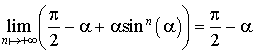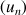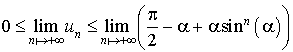a. La fonction sinus est croissante sur 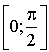 et
et
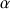 est un réel de
est un réel de 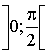 , donc pour tout
, donc pour tout 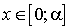 , on a
, on a 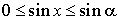 .
.
La fonction 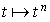 est croissante sur
est croissante sur
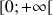 , donc
, donc 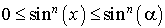 .
.
Comme 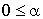 , on en déduit que :
, on en déduit que : 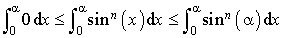
0 et 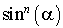 étant des constantes, on obtient :
étant des constantes, on obtient : 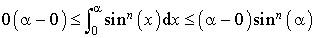 , c'est-à-dire
, c'est-à-dire 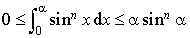 .
.
On a donc 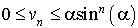 pour tout
pour tout 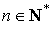 .
.
La fonction sinus est croissante sur 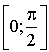 , et
, et
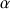 est un réel de
est un réel de 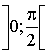 , donc pour tout
, donc pour tout 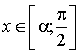 , on a
, on a 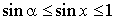 .
.
La fonction 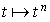 est croissante sur
est croissante sur
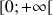 , donc
, donc 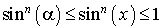 .
.
Comme 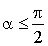 , on en déduit que :
, on en déduit que : 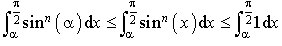 .
.
1 et 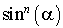 étant des constantes, on obtient :
étant des constantes, on obtient : 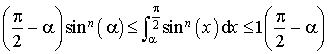 .
.
Comme on a de plus 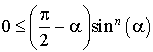 , on en déduit :
, on en déduit : 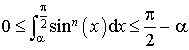 .
.
On a donc 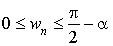 pour tout
pour tout 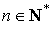 .
.
c.
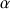 est un réel de
est un réel de 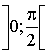 , donc
, donc 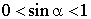 .
.
On sait que, si
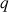 est un réel tel que
est un réel tel que
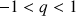 , on a
, on a 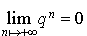 .
.
Donc 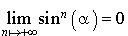 , donc
, donc 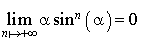 et par conséquent
et par conséquent 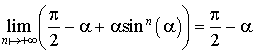 .
.
On sait que
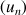 est une suite convergente ; l'inégalité
est une suite convergente ; l'inégalité 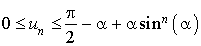 pour tout
pour tout 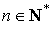 , permet alors de déduire que :
, permet alors de déduire que : 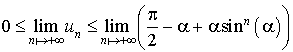 .
.
En notant
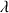 la limite de la suite
la limite de la suite
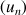 , on obtient donc :
, on obtient donc : 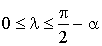 .
.
L'inégalité 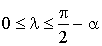 qui est justifiée pour toute valeur de
qui est justifiée pour toute valeur de
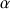 dans l'intervalle
dans l'intervalle 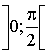 , permet de justifier, en prenant
, permet de justifier, en prenant
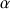 aussi proche que l'on veut de
aussi proche que l'on veut de 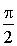 que
que
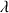 est égal à 0.
est égal à 0.
En effet, supposons que
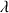 est strictement positif, on a alors :
est strictement positif, on a alors : 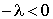 , donc
, donc 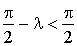 .
.
Considérons un réel
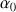 strictement positif tel que
strictement positif tel que 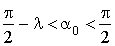 ,
,
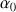 est donc un élément de
est donc un élément de 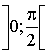 .
.
L'inégalité 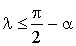 démontrée précédemment pour tout réel
démontrée précédemment pour tout réel
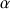 dans
dans 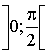 peut s'appliquer à
peut s'appliquer à
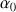 . On en déduit
. On en déduit 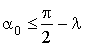 , ce qui conduit à une contradiction puisqu'on a choisi
, ce qui conduit à une contradiction puisqu'on a choisi 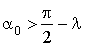 .
.
On ne peut donc pas supposer que est strictement positif.
Et comme on sait que 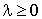 , on en déduit que
, on en déduit que 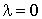 .
.
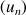 de nombres réels définie, pour tout entier naturel
de nombres réels définie, pour tout entier naturel
 non nul, par :
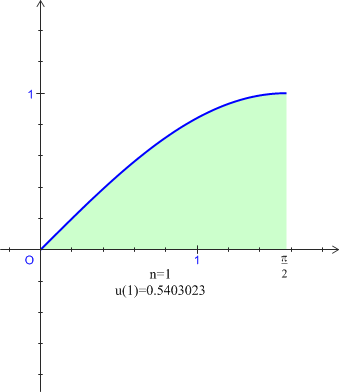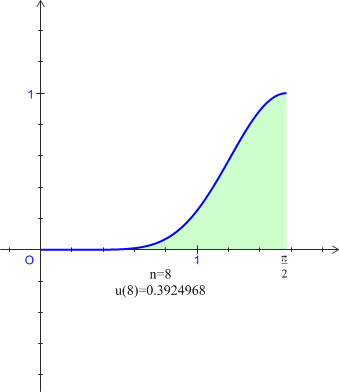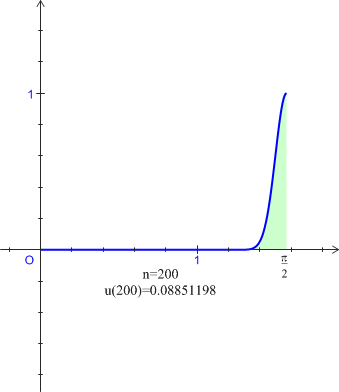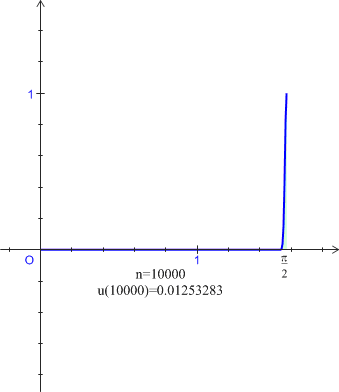
non nul, par : ![]() .
.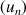 est décroissante et convergente.
est décroissante et convergente.![]() et on se propose de calculer
et on se propose de calculer
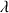 .
.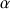 de l'intervalle
de l'intervalle ![]() et on définit les suites
et on définit les suites
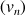 et
et
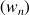 par :
par : non nul,
non nul, 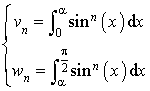 .
. non nul :
non nul : ![]() et
et ![]() .
. non nul, l'encadrement :
non nul, l'encadrement : ![]() .
.![]() . En déduire que
. En déduire que
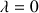 .
.