Définition
Soient
| 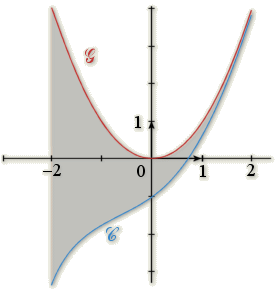 |
![]() est la représentation graphique d'une fonction
est la représentation graphique d'une fonction
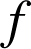 et
et ![]() celle d'une fonction
celle d'une fonction
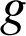 .
.
L'aire en unités d'aire de la surface grisée est égale à ![]() .
.
Soient
|  |
![]() est la représentation graphique d'une fonction
est la représentation graphique d'une fonction
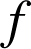 et
et ![]() celle d'une fonction
celle d'une fonction
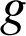 .
.
L'aire en unités d'aire de la surface grisée est égale à ![]() .
.