Soit
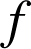une fonction définie continue sur un intervalle
:
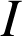Définition
Relation de Chasles
Pour tous réels
,
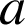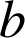et
de
, 
.
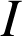Exemple
Si
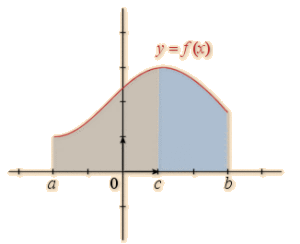|  Interprétation graphique |
Conséquences
Pour tout réel
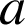de
, 
.
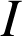Pour tous réels
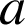et
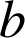de
, 
.
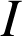