Soit 
, 
et 
.
Exprimer en fonction de
,
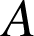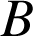et
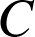les intégrales suivantes :
Puis, calculer
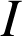et
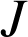(on admettra que
).
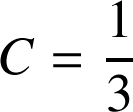Soit , et .
Exprimer en fonction de
,
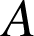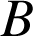et
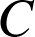les intégrales suivantes :
Puis, calculer
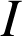et
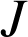(on admettra que
).
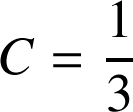