Dérivée et sens de variation
Théorème :
Soit
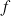une fonction dérivable sur un intervalle
.
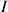Si
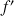est nulle sur
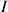, alors
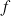est constante sur
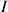.Si
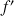est strictement positive sur
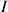, sauf en des points isolés, alors
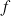est strictement croissante sur
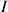.Si f' est strictement négative sur I, sauf en des points isolés, alors f est strictement décroissante sur I.
Exemple : Sens de variation de la fonction cube
La fonction 
est dérivable sur R et sa dérivée 
est strictement positive sur R, sauf en 0.
On en déduit que la fonction cube est strictement croissante sur R.
