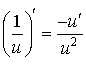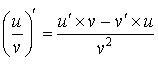Règles de dérivation
Définition : Dérivée d'une somme, d'un produit, d'un quotient
Soient
et
deux fonctions dérivables sur un intervalle
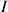et soit
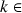R, alors les fonctions 
, 
, 
, 
, 
sont dérivables en tout point de leur ensemble de définition et on a :
Définition : Dérivée d'une composée
Soit
une fonction dérivable sur un intervalle
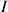et
une fonction dérivable sur un intervalle
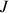tel que pour tout
, 
,
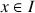alors 
est dérivable sur
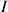et 
Définition : Cas particuliers
Soit
une fonction dérivable sur un intervalle
.
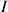Soit
un entier, 
,
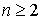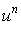est dérivable sur
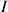et :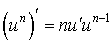 
.En particulier pour
: 
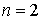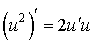.Soit
un entier,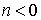 
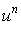, est dérivable sur tout intervalle
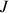contenu dans
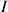et dans lequel
ne s'annule pas et : .
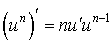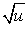est dérivable sur tout intervalle
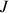contenu dans
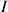et dans lequel
est strictement positive et :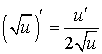 
.
, 
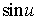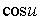sont dérivables sur
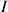et :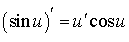 
, 
.
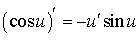Exemple :
Justifions que la fonction 
est dérivable sur R et calculons sa dérivée.
La fonction u définie sur
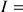R par 
est dérivable sur R, et on a 
.
La fonction
définie sur
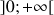par 
est dérivable sur
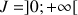et on a 
.
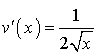De plus, pour tout réel
on a 
, donc .
On en déduit que la fonction 
est dérivable sur R et sa dérivée est donnée par 
,
c'est-à-dire que pour tout réel
, 
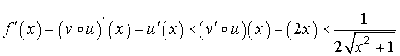
donc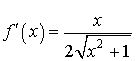 
pour tout
appartenant à
.
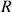