Dérivée
Définition : Nombre dérivé
Soit
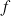une fonction définie sur un intervalle
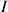et soit
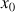appartenant à
.
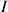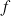est dérivable en
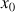si 
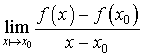existe et appartient à R.
On notera alors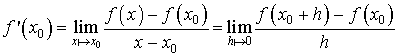 
.
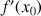est le nombre dérivé de
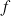en
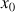, c'est le coefficient directeur de la tangente à la courbe
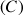de
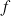au point d'abscisse
.
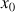Définition : Fonction dérivée
Soit
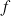une fonction définie sur un intervalle
,
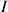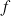est dérivable sur
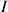si
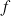est dérivable en tout
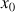de
.
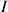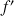est la fonction dérivée de
.
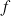Définition : Continuité d'une fonction dérivable
Une fonction dérivable en
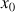est continue en
.
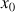