L'espace est muni d'un repère orthonormal 
.
Soient les droites :
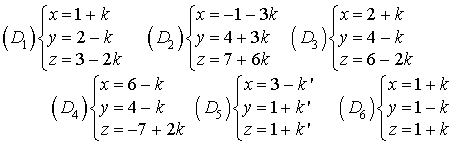
Étudier la position relative de
avec chacune des droites
,
,
,
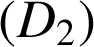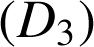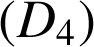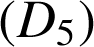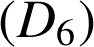et
.
-
et
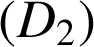sont confondues.
La droite
passe par le point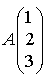 
et a pour vecteur directeur 
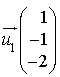.La droite
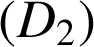passe par le point 
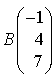et a pour vecteur directeur 
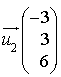.Comme
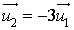, les droites sont parallèles. Le point
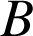appartient à
car il existe un réel
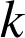tel que 
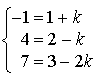(ce réel est évidemment
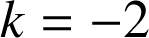).Donc les droites sont parallèles, elles ont un point commun, donc elles sont confondues.
-
et
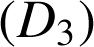sont strictement parallèles.
La droite
passe par le point 
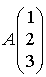et a pour vecteur directeur 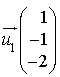.La droite
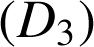passe par le point 
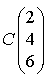et a pour vecteur directeur 
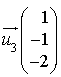.Les vecteurs
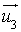et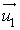 
sont colinéaires : les droites
et
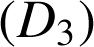sont donc parallèles. Si elles étaient confondues, le point
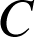appartiendrait à
, donc il existerait un réel
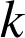tel que 
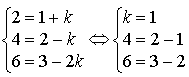, ce qui est évidemment impossible.Donc
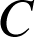n'appartient pas à
, et donc
et
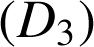sont strictement parallèles. -
et
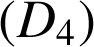sont sécantes.
La droite
a pour vecteur directeur 
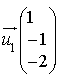.La droite
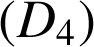a pour vecteur directeur 
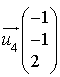.Les vecteurs
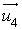et 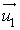ne sont pas colinéaires : les droites sont sécantes ou non coplanaires.Cherchons si
et
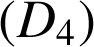ont un point commun, c'est-à-dire s'il existe deux réels
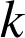et
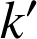tels que :
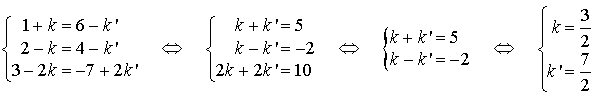
En remplaçant
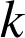par
dans l'équation de
, on obtient le point 
.
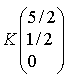(On obtient bien sûr le même point en remplaçant
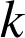par
dans l'équation de
).
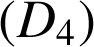et
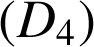sont sécantes en
.
-
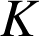et
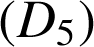ne sont pas coplanaires.
La droite
a pour vecteur directeur 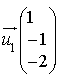.La droite
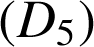a pour vecteur directeur 
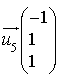.Les vecteurs
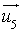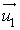et ne sont pas colinéaires : les droites sont sécantes ou non coplanaires.Cherchons si
et
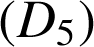ont un point commun, c'est-à-dire s'il existe deux réels
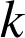et
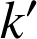tels que :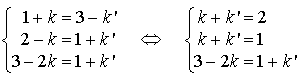
Ce système n'a pas de solution. Les droites
et
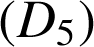sont disjointes, non parallèles et donc non coplanaires. -
et
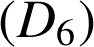sont perpendiculaires et ne sont pas coplanaires.
La droite
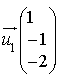a pour vecteur directeur .La droite
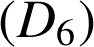a pour vecteur directeur 
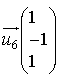.Les vecteurs
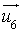et 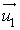ne sont pas colinéaires : les droites sont sécantes ou non coplanaires.De plus
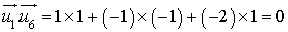.Les vecteurs
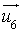et 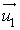sont donc orthogonaux, les droites sont perpendiculaires.Cherchons si
et
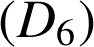ont un point commun, c'est-à-dire s'il existe deux réels
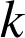et
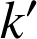tels que :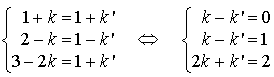
Ce système n'a pas de solution. Les droites
et
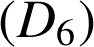sont disjointes.
