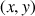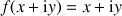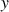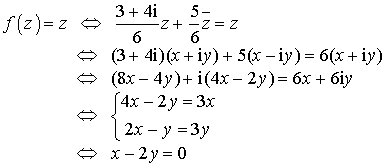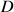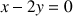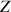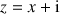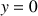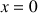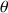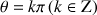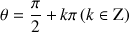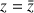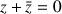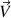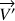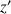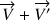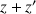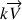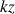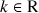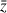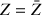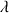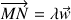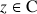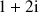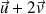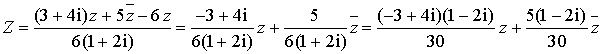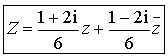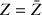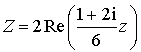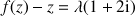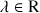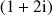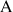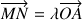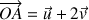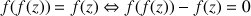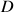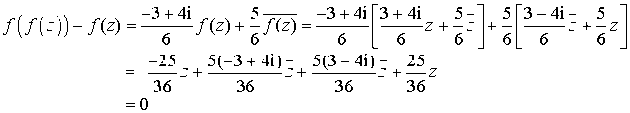Recherche de l'interprétation géométrique d'une application complexe
Introduction
Prérequis :
Caractérisation d'une droite par un point et un vecteur directeur
Projection d'un point sur une droite parallèlement à une direction
Durée : 60 minutes
Le plan complexe est rapporté à un repère orthonormal direct 
; on considère le point
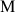d'affixe
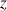et le point
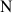d'affixe
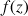avec 
où
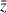est le conjugué de
.
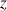Le but de l'exercice est de construire géométriquement le point
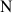à partir du point
.
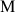1) Déterminer l'ensemble
des points
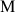tels que
.
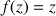2) Exprimer le nombre
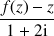en fonction de
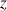et de
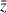et justifier que ce nombre est réel.
En déduire que le point
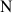appartient à la droite
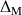passant par
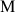et de vecteur directeur
.
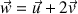3) Montrer que pour tout nombre complexe
,
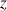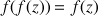. En déduire que le point
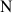est le point d'intersection de
et de
.
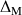4) Enoncer la construction géométrique de
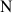à partir de
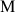; caractériser l'application géométrique du plan qui à
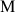associe
.
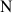