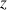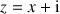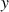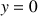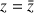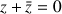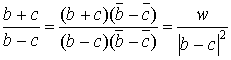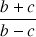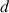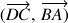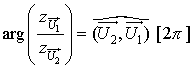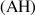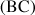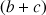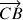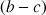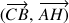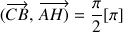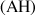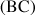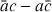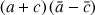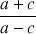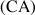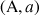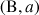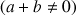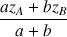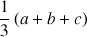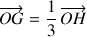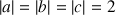Un résultat de géométrie...
Introduction
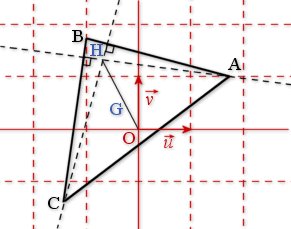
L'objectif de cette exercice est d'obtenir le résultat de géométrie suivant :
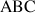un triangle et
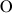le centre de son cercle circonscrit, le point
défini par
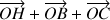est l'orthocentre de
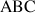. Dans un triangle, l'orthocentre, le centre de gravité et le centre du cercle circonscrit sont alignés.
Prérequis :
Vecteurs, angle de vecteurs
Hauteur, centre de gravité et orthocentre dans un triangle
Durée : 50 minutes
Le plan complexe est rapporté à un repère orthonormal direct 
(unité graphique : 4 cm).
On considère les 3 nombres complexes non nuls deux à deux distincts
,
,
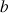tels que
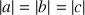. On désigne par
,
,
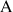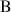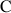les points d'affixes respectives
,
,
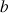et
le point d'affixe
.
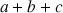1) Soit
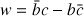. Démontrer que
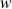est un imaginaire pur et en déduire que
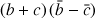et
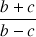le sont aussi.
2) Exprimer en fonction de
,
,
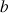, les affixes des vecteurs
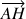et
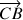et en déduire que
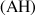est une hauteur du triangle
.
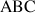Justifier que
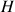est l'orthocentre du triangle
.
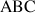3)
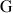est le centre de gravité du triangle
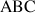; après avoir précisé son affixe, justifier l'alignement des points
,
,
.
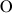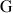4) Dans cette question,
,
,
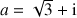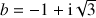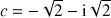; faire la figure et placer
et
.
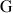