On suppose maintenant que le domaine 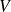peut être décrit par :

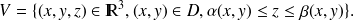
L'expression de l'intégrale triple par la méthode des bâtons est la suivante :

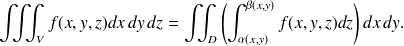
Le domaine plan 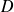est la projection orthogonale de 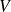sur le plan 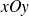. On pourrait dire que 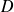est l'ombre de 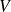sur le plan 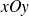, si on éclaire 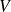parallèlement à .

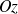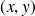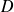Soit un point de coordonnées dans , on considère alors la droite parallèle à 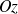et qui passe par ce point. Cette droite coupe le domaine 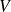en deux points dont les cotes sont notées 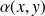et 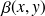conformément à la figure.

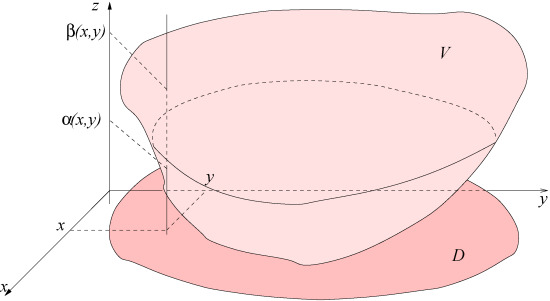
En fait 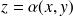est la surface qui limite le domaine 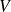vers le bas (la surface à l'ombre si l'on reprend l'éclairage parallèlement à 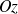). 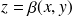est la surface qui limite le domaine 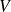vers le haut (la surface éclairée).

Une manière imagée d'expliquer cette deuxième méthode est de dire que l'on découpe le domaine en "bâtons" (penser à une pomme de terre découpée en frites !) d'où le nom de méthode "bâtons" de calcul de l'intégrale triple.

On aurait aussi, en privilégiant l'axe

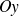
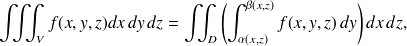
où 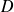est la projection de 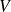dans le plan 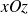et 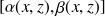est l'intersection de la droite parallèle à 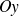passant par le point 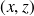du domaine 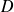avec .

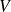Si le domaine 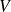est symétrique par rapport au plan d'équation 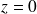( le plan 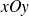), si la fonction 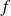est impaire en 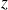(c'est à dire ), alors :

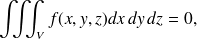
en effet dans ce cas 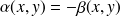, en utilisant les propriétés de l'intégrale simple .

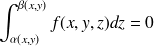Des résultats similaires en et 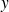peuvent être énoncés.