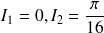Calculer
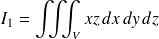 et
et
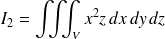 où
où
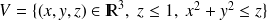
en utilisant la méthode des bâtons et la méthode des tranches.
Réponses :
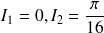
Calculer
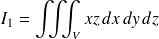 et
et
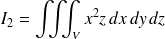 où
où
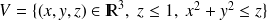
en utilisant la méthode des bâtons et la méthode des tranches.
Réponses :