Cas des écoulements non permanents
Cas de l'écoulement rotationnel
On considère l'écoulement d'un fluide parfait, les forces de volume agissant dérivent d'un potentiel, l'écoulement est non permanent.
On écrit l'équation d'Euler :
En tenant compte des hypothèses, et en développant l'expression de l'accélération, on obtient :
On calcule la circulation de l'expression précédente entre M1 et M2.
Démonstration
Cas particulier
Cas où la section du filet de courant est constante :
Le fluide est incompressible, il y a donc conservation du débit en volume (
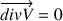), comme la section est constante, la vitesse l'est également :
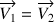. A chaque instant
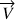et
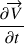ont la même valeur le long de la ligne de Courant.
