Ecoulement conservatif
Écoulement conservatif (sans production de fluide)
Faisons le bilan des masses :
Masse totale sortant de la surface S par unité de temps:
Dans l'élément de volume
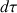et pendant le temps dt, la variation de masse est égale à :
Dans le volume
et pendant l'unité de temps, il s'accumule :
Donc au total :
Cette équation représente la forme globale ou intégrale du principe de conservation de la masse
On considère que dans le volume V il n'y a pas de discontinuité et que l'élément de volume est quelconque, on peut donc écrire :
Cette équation représente la forme locale du principe de conservation de la masse.
