Tenseur des contraintes et tenseur des taux de déformation
Tenseur des contraintes
Dans un fluide visqueux, les forces de contact entre les éléments fluides comprennent à la fois les forces de pression et des cissions dues à la viscosité. Les cissions dépendent du taux de déformation des particules de fluide. On admet qu'elles résultent d'échange de quantité de mouvement à l'échelle moléculaire entre des particules ayant des vitesses différentes.
Le tenseur des contraintes
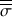peut se décomposer en la somme d'un tenseur sphérique
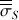et d'un tenseur déviateur
de trace nulle.
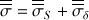
Tenseur des contraintes
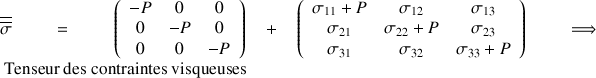
Cette relation peut se noter :
Dans le cas du fluide parfait, σij = 0 et σii = -P, le tenseur des contraintes se réduit donc au premier terme.
Forces de contact
La résultante des forces de contact est :
Soit en utilisant le théorème de la divergence :
On obtient par unité de volume :
La résultante des forces de contact est égale à la divergence du tenseur des contraintes
Tenseur des taux de déformation
Ce tenseur a été introduit en cinématique
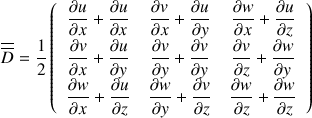
Dans cette expression, u, v, w sont les composantes de la vitesse dans un référentiel O, x, y, z
Remarque :
la trace de ce tenseur est égale à la divergence de la vitesse (div
)
