Introduction à la biologie de l'évolution

Dans certaines conditions, une loi simple régit le rapport entre les fréquences alléliques et les fréquences phénotypiques / génotypiques. Cette loi a été mise en évidence de façon concomitante par 2 scientifiques européens, Godfrey Harold Hardy (1877 - 1947), mathématicien anglais et Wilhelm Weinberg (1862 - 1937), médecin allemand.

Les conditions nécessaires à l'application de cette loi sont :

• la population considérée doit appartenir à une espèce diploïde à reproduction sexuée

• le gène considéré doit être autosomique

• ses générations doivent être non chevauchantes

• elle doit être de taille infinie

• il ne doit exister aucune migration (pas de mélange avec d'autres populations)

• Le taux de mutation (transformant les allèles A en a ou réciproquement) est considéré comme nul

• aucune sélection ne doit exister pour le caractère étudié

• La population doit se reproduire en panmixie et/ou en pangamie

Prenons le cas d'une population analysée pour un locus autosomique A à deux allèles « A » et « a » à des fréquences respectives p et q.

f(A) = p ; f(a) = q avec p + q = 1

Si les conditions énumérées au-dessus sont réalisées, alors la fréquence des gamètes (g) mâles ou femelles portant l'allèle A vaut p et celle des gamètes portant a vaut q.

f(gA) = p ; f(ga) = q

La rencontre des gamètes découlant de la panmixie est aléatoire et ne dépend donc que de la fréquence de ceux-ci.

Un tableau illustrant cette rencontre peut être construit :

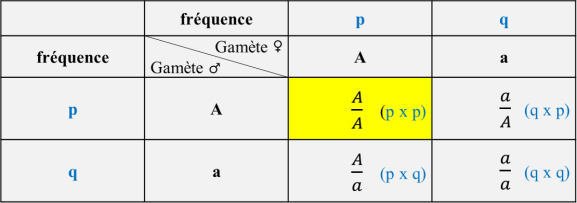
Illustrons le principe en analysant l'origine de la case jaune. Imaginons un sac contenant les gamètes mâles et un autre contenant les gamètes femelles. La probabilité de tirer dans le premier sac un gamète A (sans possibilité de choisir et simplement par le fait du hasard) est donc équivalente à sa fréquence dans le sac soit p. Il en est de même pour le sac des gamètes femelles. Ces deux événements sont indépendants. Les lois de probabilités nous disent :

- Si deux événement E et F sont indépendants alors p(E ∩ F) = p(E) x p(F)

La superposition des deux événements produira un individu A/A avec une probabilité valant donc p x p = p². Le raisonnement est le même pour les autres cases du tableau. On peut donc établir la répartition des 3 génotypes dans la descendance comme suit :

• f(A/A) = p²

• f(a/a) = q²

• f(A/a) = 2pq

La somme des fréquences des différentes classes fait bien sûr 1, on peut le vérifier :

• p² +2pq + q² = (p + q)² = 1² = 1 (identité remarquable)

Que devient la fréquence des allèles à cette génération ? Rappelons-nous le calcul effectué précédemment :

• f(A) = f(A/A) + ½ f(A/a) = p²+ ½ (2pq) =p² + pq =p(p+q) = p puisque p+q = 1

• f(a) = f(a/a) + ½ f(A/a) = q²+ ½ (2pq) =q² + pq =q(p+q) =q puisque p+q = 1

La fréquence des allèles ne change pas d'une génération à l'autre. Les conditions initiales maintenues, l'équilibre de H-W est maintenu au cours des générations.