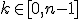Racines nèmes d'un nombre complexe
Déterminer:
les racines quatrièmes de 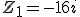
les racines sixièmes de 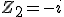
les racines troisièmes de 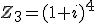
Racines quatrièmes de 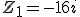
On met -16i sous forme exponentielle
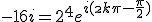
On cherche les nombres complexes 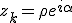 tels que
tels que 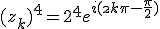
Ce qui donne 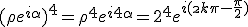
En égalant les modules et les arguments on obtient
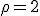
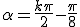
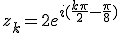
|
Les racines quatrièmes de -16 i sont :
|
|
|
Racines sixièmes de 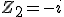
On met 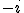 sous forme exponentielle
sous forme exponentielle
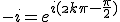
On cherche les nombres complexes 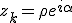 tels que
tels que 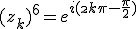
Ce qui donne 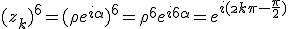
En égalant les modules et les arguments on obtient
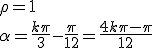
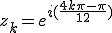
|
|
|
|
Racines troisièmes de 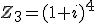
On met (1+i)4 sous forme exponentielle
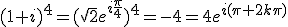
On cherche les nombres complexes 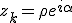 tels que
tels que 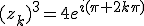
Ce qui donne 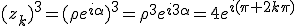
En égalant les modules et les arguments on obtient
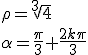
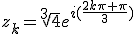
|
Les racines troisièmes de
Les racines troisièmes de
|
|
|
Rappel
|
Recherche des racines nème du nombre complexe
On cherche les k nombres complexes
Posons:
Deux nombres complexes sont égaux s'ils ont même module et si leurs arguments sont égaux à En écrivant l'égalité des modules on obtient :
En écrivant l'égalité des arguments à 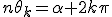
Ce qui peut s'écrire
Les n racines nème du nombre complexe
|
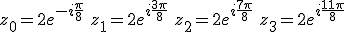
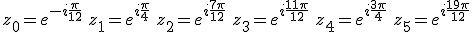
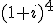 sont sous forme exponentielle :
sont sous forme exponentielle :
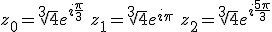
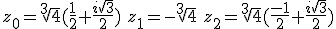
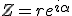
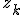 tels que
tels que
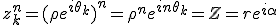
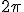 près.
près. 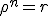
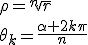
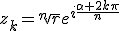 avec
avec