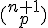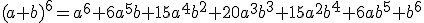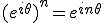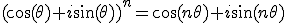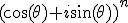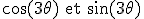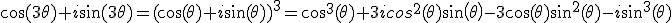Formule de Moivre
Exprimer cos(7x) et sin(7x)en fonction de cos(x) et sin(x).
cos(7x)+isin(7x)=(cos(x)+isin(x))7
On utilise le triangle de Pascal pour caculer les coefficients de (a+b)7
cos(7x)+isin(7x)=(cos(x+isin(x))7 = cos7x+7icos6(x)sin(x)-21cos5(x)sin2(x)-35icos4(x)sin3(x)+35cos3(x)sin4(x)+21icos2(x)sin5(x)-7cos(x)sin6(x)-isin7(x)
en égalant partie réelle et partie imaginaire on obtient :
cos(7x)= cos7(x)-21cos5(x)sin2(x)+35cos3(x)sin4(x)-7cos(x)sin6(x)
sin(7x)=7cos6(x)sin(x)-35cos4(x)sin3(x)+21cos2(x)sin5(x)-sin7(x)
|
Triangle de Pascal
Le triangle de Pascal est basé sur la propriété des coefficients
Exemple :
|
|
Formule de Moivre
On développe à l'aide de la formule du binôme de Pascal
On utilise les deux relations ci-dessous pour obtenir
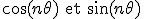
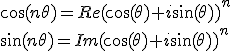
Exemple
Calcul de
On en déduit 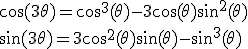
|
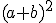
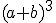
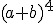
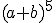
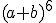
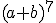
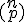 du binôme ci-dessous :
du binôme ci-dessous :
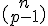 =
=