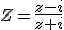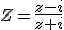Domaine de définition de Z : z doit appartenir à C-{-i}
Z réel
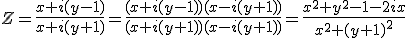
Z réel si et seulement si x=0
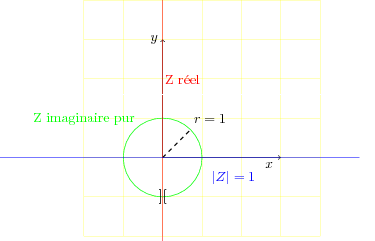
L'ensemble des points M tels que Z soit réel est l'axe des y privé du point (0,-1)
Z imaginaire pur
Z imaginaire pur si et seulement si
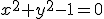 ce qui est le cercle de centre O et de rayon 1
ce qui est le cercle de centre O et de rayon 1
L'ensemble des points M tels que Z soit imaginaire pur est le cercle de centre O, de rayon 1 privé du point (0,-1)
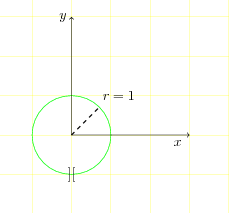
Module de Z égal à 1
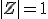 équivaut à
équivaut à 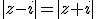
l'ensemble des points M tels que module de Z soit égal à 1 est la médiatrice de [AB] avec A=(0,1) B=(0,-1)
c'est donc l'axe des x .
L'ensemble des points M tels que module de Z soit égal à 1 est l'axe des x
| Les différents ensembles de points |
 |