Filtre de Chebychev
Les filtres de Chebychev sont, comme les filtres de Butterworth, des filtres polynomiaux : les passe-bas sont caractérisés par un polynôme au dénominateur et par une constante au numérateur. Par rapport aux filtres de Butterworth, les filtres de Chebychev se caractérisent à ordre équivalent par une pente plus raide dans la bande rejetée : en contrepartie, ils présentent une ondulation du gain dans la bande passante.
Le filtre passe-bas de Chebychev d'ordre n est défini par le module au carré de sa fonction de transfert selon :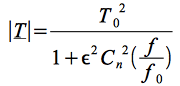 
où 
est défini par une relation de récurrence, 
et où le taux d'ondulation dans la bande passante est fixé par le paramètre réel, 
. Dans la pratique, on utilise trois valeurs d'ondulation, 0.1 dB, 0.5 dB et 1 dB.
La théorie qui permet d'aboutir aux polynômes des filtres en fonction de son ordre n'est pas étudiée ici, on se contentera de consigner les résultats dans des tableaux, un tableau par taux d'ondulation ci-dessus et ce, pour les ordres de 2 à 5.
Comme précédemment, il s'agit là de fonctions de transfert normalisées, la variable complexe est définie par 
:
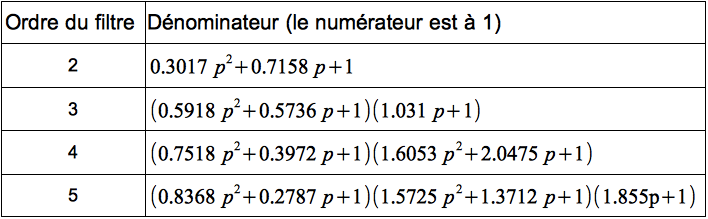
Table des polynômes normalisés pour 
Table des polynômes normalisés pour 
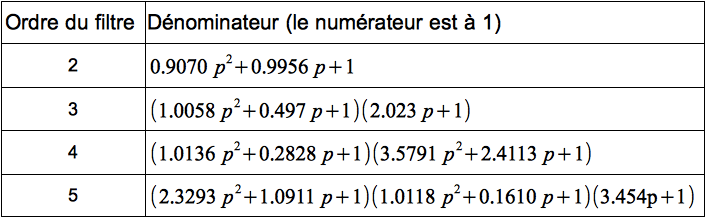
Table des polynômes normalisés pour
A titre d'exemple, la fonction de transfert du passe-bas de Chebychev du cinquième ordre avec une ondulation de est tracée ci-dessous avec le concours du logiciel scilab. Le lecteur est encouragé à tracer différentes fonctions de transfert et à les comparer à celles des filtres de Butterworth.
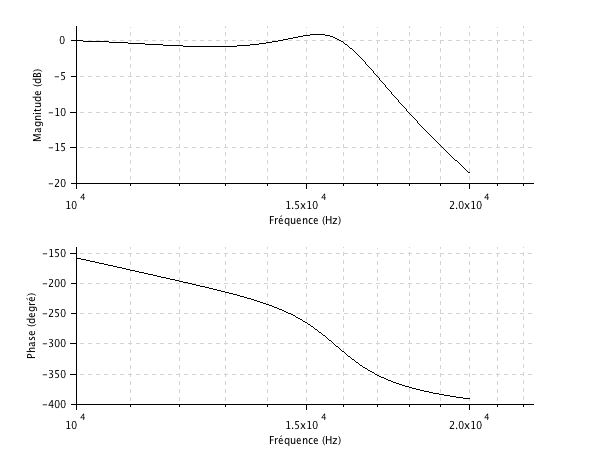
Une fois la fonction de transfert déterminée, la détermination des composants d'une structure de Rauch ou de Sallen-Key qui l'incarne se fait de manière tout à fait analogue à ce qui a été fait dans ces paragraphes
Les filtres de Chebychev ont leur principal intérêt dans leur pente. A ordre n donné, c'est le type de filtre qui a la pente la plus raide dans la bande passante. Cet avantage se fait au détriment de l'ondulation dans la bande passante (d'autant plus importante que sa pente dans la bande rejetée est raide) et aussi au détriment du délai de groupe varie beaucoup dans la bande passante.
