Le filtre de Butterworth
On rappelle que seule l'étude théorique du filtre passe-bas est faite. On passe aux autres types, passe-haut, etc.. par changement de variable.
Le filtre de Butterworth d'ordre n est défini par le module au carré de sa fonction de transfert selon : 
On montre aisément que quel que soit l'ordre n du filtre, le gain à la fréquence 
est toujours de -3 dB. On admettra que c'est le filtre de Butterworth qui permet sur l'ensemble des types standardisés de filtres d'obtenir la réponse la plus plate dans la bande passante.
La problématique théorique du filtre de Butterworth consiste à établir pour un ordre n donné, la fonction de transfert complexe qui aboutit à la définition du filtre, soit :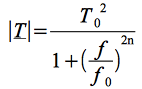 
On ne traitera pas ici cette question qui relève de l'analyse des fonctions complexes et on se contentera de donner sous forme de tableau de synthèse les résultats en fréquences ou pulsations normalisées (la variable complexe est définie par 
pour les ordres 2 à 6 :
Du point de vue opérationnel, si on choisit un filtre passe-bas de Butterworth d'un ordre donné pour satisfaire à un gabarit cahier des charges, il s'agira de déterminer les cellules (de Rauch ou de Sallen-Key, par exemple) qui incarneront les polynômes du tableau ci-dessus. Par exemple, pour l'ordre 4, il s'agit de cascader deux cellules de Rauch, par exemple, avec les polynômes suivants : 
en rappelant qu'ici, la variable complexe est normalisée en pulsation. En d'autres termes, la fonction de transfert s'écrit, en pulsation :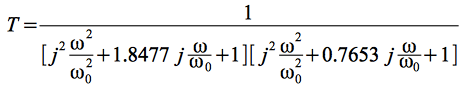 
Le diagramme de Bode ci-dessous a été tracé avec Scilab :
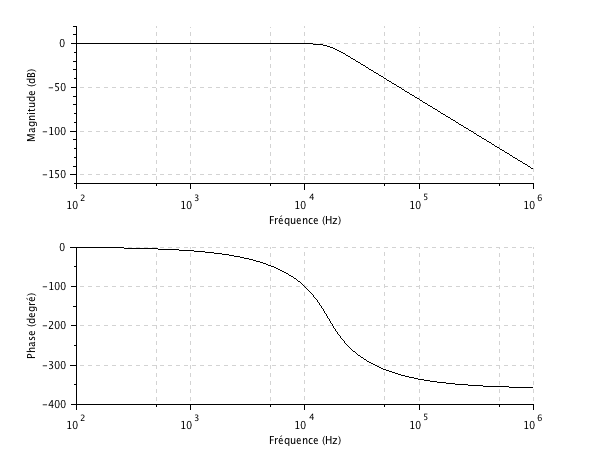
On rappelle que pour la structure ou cellule de Rauch : 
, 
et
. Or, on veut d'une part 
, pour le premier polynôme au dénominateur et 
pour le second et on veut pour les deux cellules identiquement 
soit 
.
On peut choisir pour le premier polynôme le jeu de composants (valeurs normalisées) suivants : 
, 
et 
.
Et pour le second : 
, 
et 
.
Évidemment, quand on réalise la cellule avec des composants discrets, il faut opter pour des valeurs normalisées (c'est le cas pour les valeurs ci-dessus) des composants résistances et condensateurs proches des valeurs qui résultent des calculs théoriques ce qui entraîne nécessairement des valeurs numériques pour 
et 2m légèrement différentes de la théorie.
On laisse au lecteur le soin de simuler le circuit avec Pspice pour confirmer le bon fonctionnement du filtre.
Le filtre de Butterworth a une réponse très plate dans la bande passante, une assez bonne performance en terme de délai de groupe mais une pente pas très raide dans la bande rejetée.
