(2) Équation aux dimensions
En mécanique des fluides, la loi de Jurin dit qu'un liquide, de masse volumique
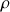, peut monter dans un tube capillaire de rayon
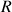jusqu'à une hauteur
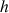. La loi de Jurin s'écrit avec la relation :
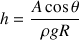
où
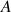est la coefficient de tension superficielle du liquide et
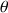l'angle de raccordement entre le liquide et le tube (on considérera que
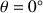). On réalise l'expérience avec des tubes capillaires de différents rayon
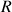et on note la hauteur atteinte
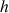. Dans un graphique
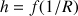les points s'alignent correctement.
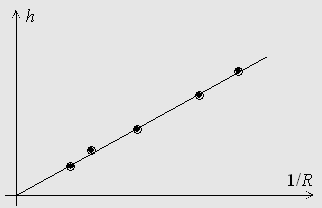
Question
Quelle est la dimension du coefficient de tension superficielle
?
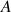Le graphique présente une relation affine entre
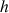et
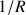: le coefficient directeur de la droite nous donne le coefficient de proportionnalité entre
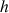et
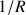. Celui-ci est :
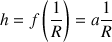
D'après la loi de Jurin pour
:
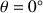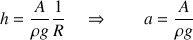
Le coefficient directeur est de dimension :
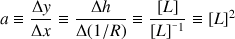c'est-à-dire une surface.
Ainsi :
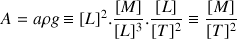
Donc le coefficient de tension superficielle devrait s'exprimer en
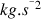. En fait la tension superficielle est une caractérisation de la force qui tend à faire monter le liquide dans le capillaire. On l'exprime alors comme une force en newton
:
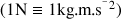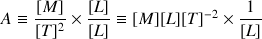
Le coefficient de tension superficielle s'exprime donc en
.
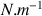