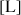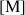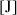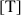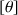Équation aux dimensions
À partir d'une expérience ou d'un calcul, on est souvent amené à déterminer une grandeur (valeur). Ces grandeurs ne sont pas seulement des nombres, mais représentent une quantification physique : la grandeur doit donc être exprimée dans un système d'unité (le Système International de préférence).
Dans un calcul, chacune des grandeurs possède une dimension (longueur, masse, temps, ...). On doit donc exprimer les grandeurs calculées en fonction de ces dimensions : on appelle cela faire de l'analyse dimensionnelle. On représente ces dimensions entre crochets sans tenir compte de l'unité :
longueur |
| intensité électrique |
|
masse |
| énergie rayonnante |
|
temps |
| quantité de matière |
|
température |
|
Exemple :
Une force s'exprime en newton. Une des forces simples est le poids
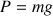, où
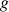est l'accélération de la pesanteur. Quelle est la dimension du poids, donc du newton ?La force de gravité entre deux corps de masses
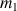et
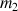séparés de la distance
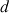est donnée par :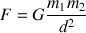
où
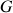est la constante de gravitation. Quelle est la dimension de
?
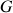SOLUTION
Le poids
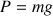s'exprime comme le produit de l'accélération de la pesanteur
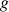par la masse
:
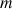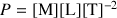
Ainsi une force s'exprime en newton et
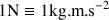.La constante de gravitation est donnée par :
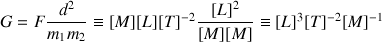
Ainsi la constante de gravitation
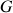s'exprime en
.
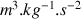