Courbe lisse interpolant des points de contrôle
Bien que l'algèbre linéaire est essentiellement associée à des objets plans ou droits, elle peut-être utilisée pour calculer des courbes qui passent par des points d'appui, des courbes d'interpolation. Dans l'exemple suivant, on calcule une courbe composée de morceaux de cubiques, qui passent par quatre points d'appui, dont les deux tangentes initiale et finale sont données et dont les tangentes aux points intérieurs se raccordent.
Les paramètres de la courbe sont trois jeux de quatre nombres qui vérifient un système linéaire qui exprime les conditions requises: Si les courbes données par
,
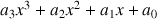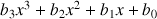et
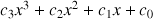sont solutions, alors, leurs paramètres vérifient le système linéaire suivant:
Le vecteur membre de droite de l'équation est composé des données du problèmes, les positions des quatre points et les deux tangentes. La première ligne de la matrice impose par exemple que la première cubique ait comme valeur en 1 l'ordonnée du premier point. Le code Mathematica suivant, où A, B, C, D, E et F sont quatre points fixés, permet de visualiser la courbe d'interpolation.
A.x=1;
B.x=2;
C.x=3;
D.x=4;
h1=(E-A).y/(E-A).x;
h2=(F-D).y/(F-D).x;
m=[
[1,1,1,1,0,0,0,0,0,0,0,0],
[8,4,2,1,0,0,0,0,0,0,0,0],
[0,0,0,0,8,4,2,1,0,0,0,0],
[0,0,0,0,27,9,3,1,0,0,0,0],
[0,0,0,0,0,0,0,0,27,9,3,1],
[0,0,0,0,0,0,0,0,64,16,4,1],
[3,2,1,0,0,0,0,0,0,0,0,0],
[12,4,1,0,-12,-4,-1,0,0,0,0,0],
[0,0,0,0,27,6,1,0,-27,-6,-1,0],
[0,0,0,0,0,0,0,0,48,8,1,0],
[12,2,0,0,-12,-2,0,0,0,0,0,0],
[0,0,0,0,18,2,0,0,-18,-2,0,0]
];
v=[A.y,B.y,B.y,C.y,C.y,D.y,h1,0,0,h2,0,0];
a=Linearsolve[m,v];
plot[x^3*a_1+x^2*a_2+x*a_3+a_4,start->1,stop->2];
plot[x^3*a_5+x^2*a_6+x*a_7+a_8,start->2,stop->3];
plot[x^3*a_9+x^2*a_10+x*a_11+a_12,start->3,stop->4];
