État d'équilibre d'un réseau de ressorts
Considérons un réseau plan de ressorts (idéaux) reliant des masses ponctuelles. Certains points sont épinglés au plan et les autres peuvent bouger librement. Une telle structure est mue par une dynamique intéressante, qui est difficile à calculer en général.
D'une manière surprenante, ce système admet une position d'équilibre bien précise que l'algèbre linéaire nous permet de calculer: Nous supposons que les ressorts ont une longueur à vide nulle. Le système évolue naturellement vers cette position d'équilibre quand nous amortissons le système avec de la friction.
À cette position, la somme des forces, en chacun des points mobiles, est nulle. La force exercée par un ressort est proportionnelle à sa raideur et à la différence des positions. Autour du point
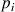, la somme des forces étendue aux points voisins
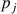, reliés par un ressort de raideur
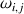, vérifie
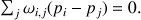
On a donc, pour
points libres, tant dans la direction
que
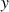, un système de
équations linéaires à
inconnues.
La position d'équilibre est ainsi, pour chacune des directions de coordonnées (ici
dans l'appliquette), la solution d'un système linéaire dont les raideurs sont les coefficients.
Dans l'appliquette ci-dessus, vous pouvez bouger les positions de départ du système, en particulier les points épinglés, régler le coefficient de frottement et lancer l'évolution dynamique en appuyant sur le bouton "lecture", jusqu'à l'équilibre, où une estimation des solutions en termes de nombres rationnels est possible en appuyant sur le bouton correspondant.
