Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
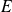 l'ensemble des séries complexes absolument convergentes.
l'ensemble des séries complexes absolument convergentes.
Pour tout
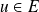 , on définit :
, on définit :
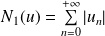 ,
,
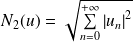 et
et
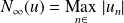 .
.
Pour tout entier
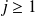 , on note
, on note
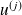 la série définie par :
la série définie par :
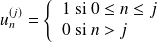 .
.
Question
Calculer
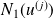 ,
,
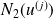 et
et
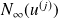 .
.
C'est une série absolument convergente puisque les sommes sont finies.
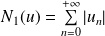 , donc :
, donc :
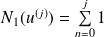 .
.
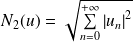 , donc :
, donc :
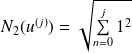 .
.
Et
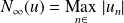 , donc :
, donc :
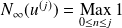 .
.
Conclusion :
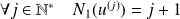 ,
,
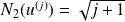 et
et
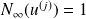 .
.
Question
Montrer que les applications
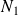 ,
,
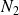 et
et
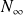 sont des normes sur
sont des normes sur
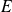 .
.
Pour chaque application, démontrez les trois axiomes.
L'ensemble
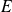 des séries absolument convergentes est un espace vectoriel sur
des séries absolument convergentes est un espace vectoriel sur
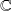 .
.
Toute série absolument convergente est bornée et de carré sommable car
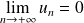 , et donc à partir d'un certain rang :
, et donc à partir d'un certain rang :
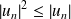 .
.
Donc les applications
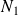 ,
,
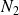 et
et
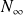 sont bien définies et sont à valeurs dans
sont bien définies et sont à valeurs dans
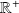 .
.
Pour toute série
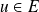 :
:
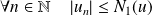 ,
,
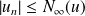 et
et
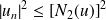 .
.Donc :
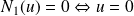 ,
,
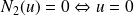 et
et
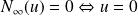 .
.
Soit
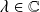 et
et
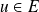 . On a :
. On a :
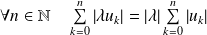 .
.Donc par passage à la limite :
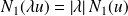 .
.De même :
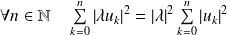 , donc par passage à la limite :
, donc par passage à la limite :
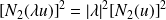 .
.Donc :
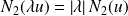 .
.Et :
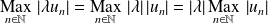 , donc
, donc
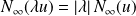 .
.
Soient
 et
et
 deux éléments de
deux éléments de
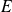 :
:
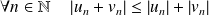 .
.Donc :
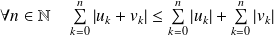 .
.Donc par passage à la limite :
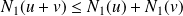 .
.Et :
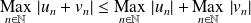 , donc :
, donc :
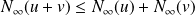 .
.Et :
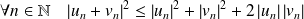 .
.Donc :
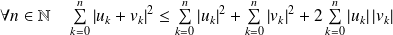 .
.Or d'après l'inégalité de Cauchy-Schwarz :
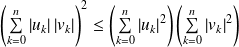 .
.Donc :
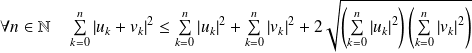 .
.Donc :
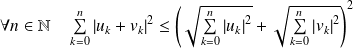 .
.Donc, par passage à la limite :
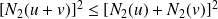 . Donc :
. Donc :
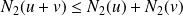 .
.
Conclusion : Les applications
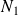 ,
,
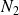 et
et
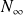 sont des normes sur
sont des normes sur
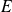 .
.
Question
Comparer ces trois normes. Sont-elles équivalentes ?
Utilisez la série
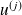 .
.
Pour toute série
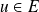 :
:
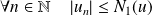 et
et
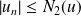 .
.
Donc :
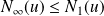 et
et
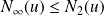 .
.
De plus :
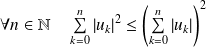 , donc :
, donc :
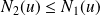 .
.
Donc :
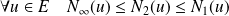 .
.
Reprenons la série définie par :
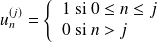 .
.
On a vu que :
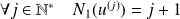 ,
,
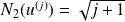 et
et
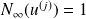 .
.
Donc :
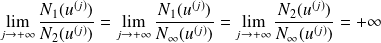 .
.
Donc aucun de ces trois quotients n'est borné.
Conclusion : Les normes
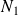 ,
,
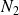 et
et
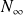 ne sont pas équivalentes, mais
ne sont pas équivalentes, mais
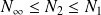 .
.





