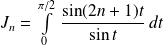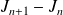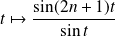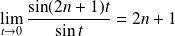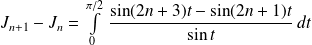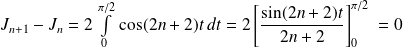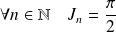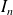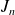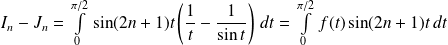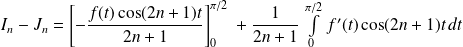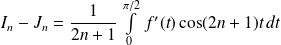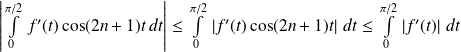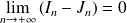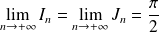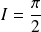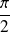Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
L'objectif est d'étudier l'intégrale de Dirichlet :
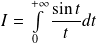 .
.
Question
Démontrer que la fonction
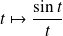 n'est pas intégrable sur
n'est pas intégrable sur
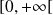 .
.
Minorez l'intégrale par la somme d'une série divergente.
La fonction
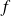 :
:
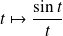 est continue sur
est continue sur
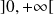 et prolongeable par continuité en
et prolongeable par continuité en
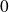 en posant
en posant
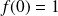 .
.
Donc il en est de même pour
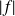 :
:
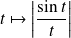 . Donc le seul problème est en
. Donc le seul problème est en
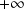 .
.
Or :
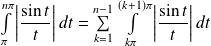 . Donc :
. Donc :
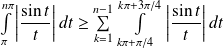 .
.
Or :
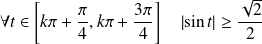 et
et
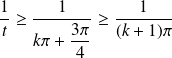 .
.
Donc :
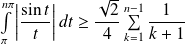 . Donc :
. Donc :
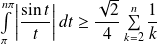 .
.
Or :
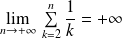 par divergence de la série harmonique
par divergence de la série harmonique
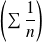 .
.
Donc :
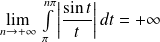 . Donc l'intégrale
. Donc l'intégrale
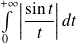 est divergente.
est divergente.
Conclusion : La fonction
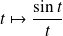 n'est pas intégrable sur
n'est pas intégrable sur
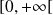 .
.
Question
Démontrer que l'intégrale de Dirichlet
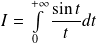 est convergente.
est convergente.
Intégrez par parties.
La fonction
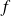 :
:
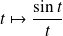 est continue sur
est continue sur
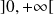 et prolongeable par continuité en
et prolongeable par continuité en
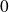 en posant
en posant
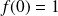 .
.
Donc l'intégrale
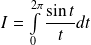 est convergente.
est convergente.
Par intégration par parties :
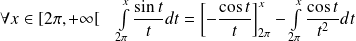 .
.
Or :
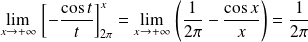 . Et :
. Et :
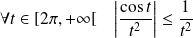 .
.
Or la fonction
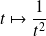 est intégrable sur
est intégrable sur
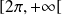 . Donc, par comparaison, la fonction
. Donc, par comparaison, la fonction
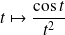 est intégrable sur
est intégrable sur
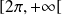 .
.
Donc l'intégrale
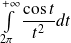 est absolument convergente donc convergente.
est absolument convergente donc convergente.
Donc la fonction
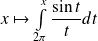 admet une limite réelle quand
admet une limite réelle quand
 tend vers
tend vers
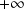 .
.
Conclusion : L'intégrale de Dirichlet
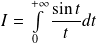 est convergente.
est convergente.
Question
En déduire la limite de l'intégrale
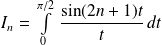 quand
quand
 tend vers
tend vers
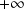 .
.
Démontrez la convergence de l'intégrale, puis effectuez un changement de variable.
La fonction
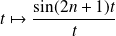 est continue sur
est continue sur
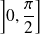 et
et
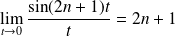 .
.
Donc l'intégrale
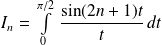 est convergente.
est convergente.
On pose :
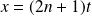 , donc
, donc
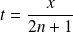 et
et
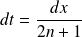 .
.
Donc :
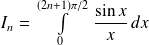 . Donc :
. Donc :
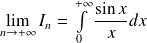 .
.
Conclusion : La limite de
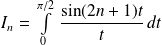 est l'intégrale de Dirichlet.
est l'intégrale de Dirichlet.
Question
Question
Démontrer que la fonction
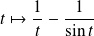 admet un prolongement en
admet un prolongement en
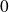 de classe
de classe
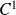 .
.
Utilisez les développements limités en
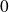 .
.
La fonction
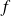 :
:
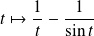 est de classe
est de classe
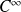 sur
sur
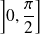 et :
et :
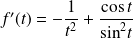 .
.
Au voisinage de
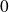 :
:
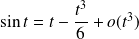 et :
et :
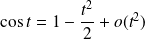 .
.
Donc :
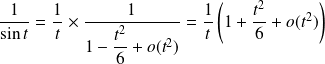 , et :
, et :
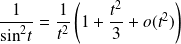 .
.
Donc :
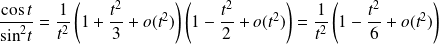 .
.
Donc :
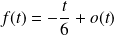 et
et
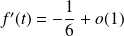 . Donc :
. Donc :
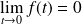 et
et
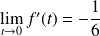 .
.
Conclusion : La fonction
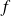 admet un prolongement de classe
admet un prolongement de classe
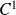 sur
sur
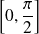 .
.
Il suffit de poser :
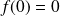 et
et
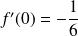 .
.