Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
L'intégrale
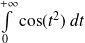est-elle absolument convergente ? semi-convergente ? divergente ?
Effectuez un changement de variable.
Pour l'absolue convergence, minorez l'intégrale par la somme partielle d'une série.
Pour la convergence, intégrez par parties.
Sur
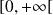, la fonction
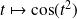est continue mais n'a pas un signe constant.
Examinons d'abord si l'intégrale est absolument convergente.
L'intégrale
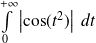est de même nature que l'intégrale
.
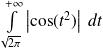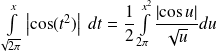en posant
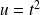, donc
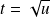et
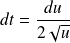.Soit
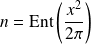. Donc :
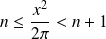, donc :
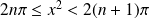.Donc :
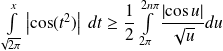. Or :
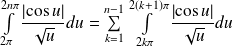.Donc :
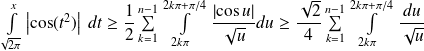.Or :
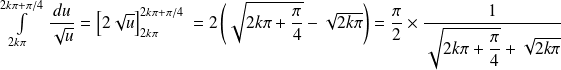.Donc :
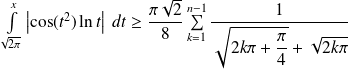.On obtient une somme partielle de la série de terme général
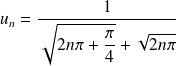.Or :
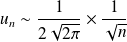. Donc la série est divergente.Donc :
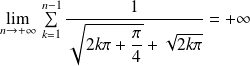. Donc :
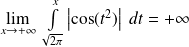.Donc les intégrales
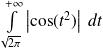et
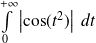sont divergentes.Conclusion : L'intégrale
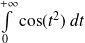n'est pas absolument convergente.
Examinons maintenant si l'intégrale est semi-convergente.
L'intégrale
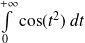est de même nature que l'intégrale
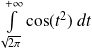.Or :
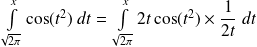. On intègre par parties.Donc :
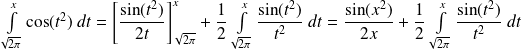.Or :
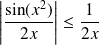. Donc :
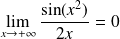.Et :
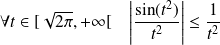. Or la fonction
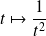est intégrable sur
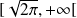.Donc l'intégrale
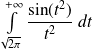est absolument convergente, donc convergente.Donc la fonction
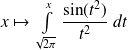admet une limite réelle quand
tend vers
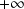.Donc les intégrales
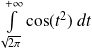et
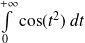sont convergentes.Conclusion : L'intégrale
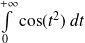est semi-convergente.
