Fonctions intégrables
Les fonctions considérées sont continues par morceaux sur un intervalle
de
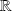à valeurs réelles ou complexes.
On se ramène aux fonctions réelles positives en utilisant le module.
Définition :
L'intégrale
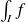d'une fonction
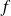continue par morceaux sur
est absolument convergente si
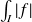est convergente.
Fondamental :
Toute intégrale absolument convergente est convergente et :
.
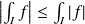Mais la réciproque est fausse : il existe des intégrales convergentes qui ne sont pas absolument convergentes.
Définition :
Une intégrale est semi-convergente si elle est convergente, mais pas absolument convergente.
Définition :
Une fonction
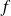continue par morceaux sur un intervalle
est intégrable sur
si son intégrale
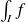est absolument convergente.
L'ensemble des fonctions continues par morceaux et intégrables sur
est noté
.
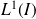On parle aussi de fonctions localement intégrables sur
, c'est-à-dire intégrables sur tout segment
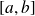inclus dans
.
Mais toute fonction continue par morceaux sur
est localement intégrable sur
.
Fondamental :
Propriétés
La somme de deux fonctions intégrables sur
est intégrable sur
.Le produit par un réel d'une fonction intégrable sur
est intégrable sur
.Le produit de deux fonctions de carrés intégrables sur
est intégrable sur
.
L'ensemble
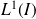est un espace vectoriel sur
.
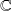On ne peut rien dire du produit de deux fonctions intégrables, mais si
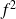et
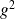sont intégrables sur
, alors
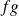est intégrable sur
.
Les propriétés suivantes sont conséquences de celles des intégrales des fonctions réelles positives.
Fondamental :
Majoration
Soient
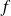et
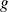deux fonctions continues par morceaux sur un intervalle
, la fonction
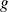étant à valeurs réelles.
Si la fonction
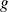est intégrable sur
et si
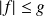, alors la fonction
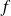est intégrable sur
.
Fondamental :
Comparaison locale
Soient
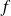et
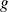deux fonctions continues par morceaux sur
(
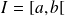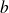réel ou infini).
Si
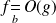et si
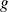est intégrable sur
, alors
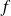est intégrable sur
.Si
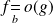et si
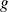est intégrable sur
, alors
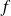est intégrable sur
.Si
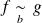, alors
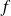est intégrable sur
si et seulement si
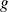est intégrable sur
.
On a évidemment des résultats analogues par comparaison en
si
.
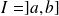