Exo 14
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions suivantes sont indépendantes.
Question
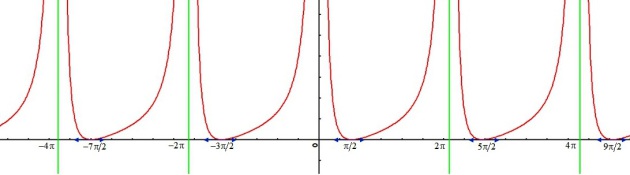
Etudier et représenter graphiquement la fonction définie par :
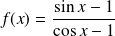 .
.
Pour l'étude des variations, exprimez
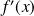 en fonction des lignes trigonométriques de
en fonction des lignes trigonométriques de
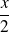 .
.
La fonction
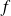 est définie si et seulement si
est définie si et seulement si
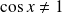 . Donc :
. Donc :
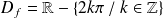 .
.
La fonction est périodique de période
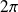 , donc on l'étudie sur
, donc on l'étudie sur
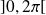 .
.
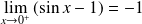 et
et
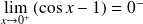 . Donc :
. Donc :
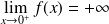 .
.
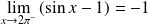 et
et
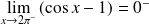 . Donc :
. Donc :
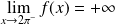 .
.
La fonction
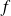 est dérivable sur
est dérivable sur
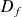 comme quotient de fonctions dérivables.
comme quotient de fonctions dérivables.
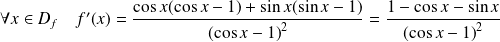 .
.
Or :
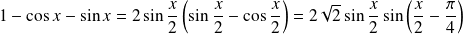 .
.
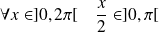 , donc :
, donc :
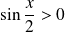 , donc
, donc
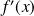 est du signe de
est du signe de
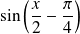 .
.
Or :
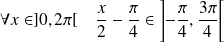 .
.
Donc :
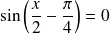 si :
si :
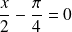 , donc si :
, donc si :
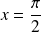 .
.
Et :
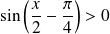 si :
si :
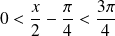 , donc si :
, donc si :
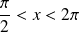 .
.
On obtient le tableau de variations de
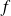 sur
sur
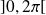 :
:
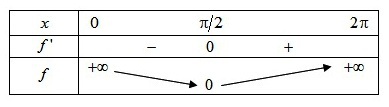
On complète la courbe par translations pour balayer tout l'ensemble de définition.
Question
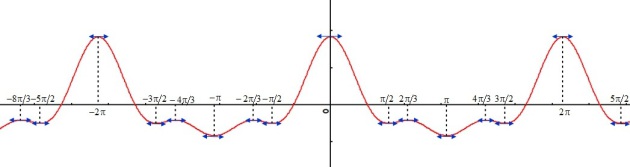
Etudier et représenter graphiquement la fonction définie par :
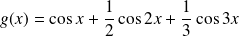
Pour l'étude des variations, transformez la somme
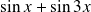 en produit.
en produit.
La fonction
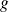 est définie sur
est définie sur
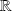 , périodique de période
, périodique de période
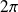 et paire. Donc on l'étudie sur
et paire. Donc on l'étudie sur
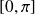 .
.
La fonction
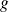 est dérivable sur
est dérivable sur
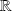 comme somme de fonctions dérivables.
comme somme de fonctions dérivables.
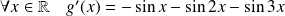 . Or :
. Or :
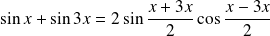 .
.
Donc :
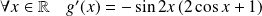 .
.
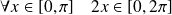 , donc :
, donc :
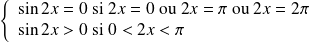 .
.
Donc :
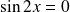 si
si
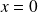 ou
ou
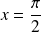 ou
ou
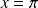 . Et :
. Et :
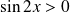 si
si
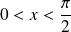 .
.
Sur
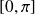 :
:
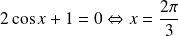 et
et
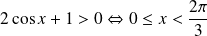 .
.
On en déduit le tableau de variations de la fonction
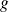 sur
sur
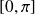 .
.
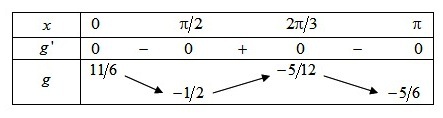
On complète la courbe d'abord par symétrie par rapport à l'axe des ordonnées, puis par translations pour balayer tout l'ensemble de définition.