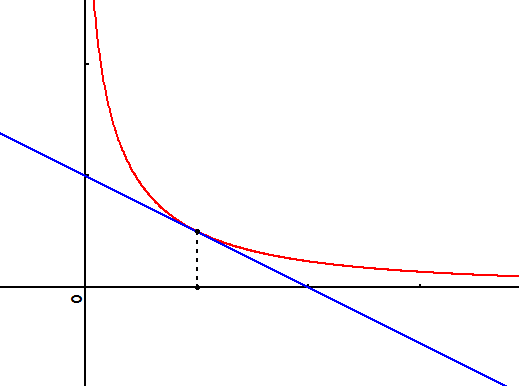
Exemple 4
Exemple :
Etudier au voisinage de
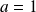la fonction définie par :
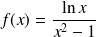si
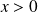et
.
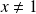Il s'agit de voir si la fonction
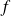est prolongeable par continuité en
, si son prolongement est dérivable en
, et éventuellement de déterminer la position de la courbe par rapport à sa tangente.
On pose
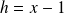, donc :
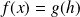avec
.
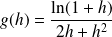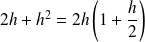. Donc :
.
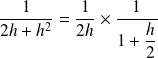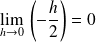et au voisinage de
:
.
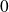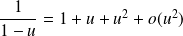Donc :
.
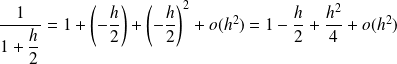Et :
.
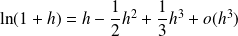Donc :
.
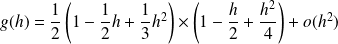Donc :
.
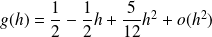Donc :
.
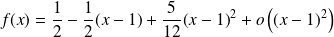Donc la fonction
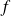admet un
.
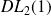On en déduit que :
.
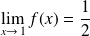Conclusion : La fonction
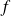est prolongeable par continuité en posant :
.
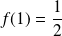Son prolongement admet un
.
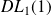Conclusion : Le prolongement de
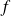est dérivable en
et
.
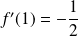Les deux premiers termes donnent une équation de la tangente.
Conclusion : Une équation de la tangente à la courbe de
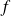au point d'abscisse
est :
.
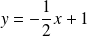Le terme non nul suivant est :
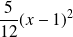, d'ordre pair avec un coefficient positif.
Conclusion : Au voisinage du point d'abscisse
, la courbe est au dessus de sa tangente en
.
