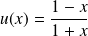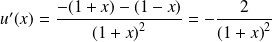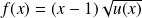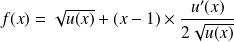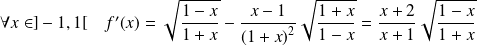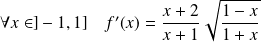Exo 4
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
 la fonction définie par :
la fonction définie par :
 .
.
Question
Déterminer l'ensemble de définition de la fonction
 .
.
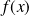 est défini si et seulement si
est défini si et seulement si
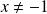 et
et
 .
.
Conclusion : L'ensemble de définition de la fonction
 est
est
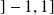 .
.
Question
Déterminer l'ensemble de dérivabilité de la fonction
 .
.
Utilisez les opérations sur les fonctions dérivables sur un intervalle.
Pour les points restants, cherchez la limite du taux d'accroissement.
La fonction
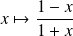 est dérivable sur
est dérivable sur
 et strictement positive sur
et strictement positive sur
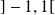 .
.
La fonction
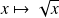 est dérivable sur
est dérivable sur
 .
.
Donc, par composition, la fonction
 est dérivable sur
est dérivable sur
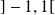 .
.
Et la fonction
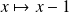 est dérivable sur
est dérivable sur
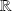 .
.
Donc, par produit, la fonction
 est dérivable sur
est dérivable sur
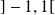 .
.
On étudie la dérivabilité en
 .
.
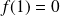 . Donc :
. Donc :
 . Donc :
. Donc :
 .
.
Donc la fonction
 est dérivable en
est dérivable en
 et
et
 .
.
Conclusion : L'ensemble de dérivabilité de la fonction
 est
est
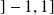 .
.