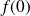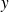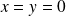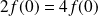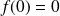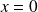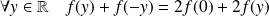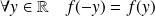Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
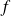une fonction continue sur
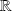qui vérifie la relation :
.
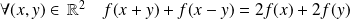Question
Question
Pour tout réel
, calculer
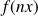en fonction de
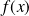pour tout entier naturel
.
Calculez
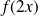et
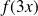en fonction de
.
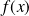Puis conjecturez une formule que vous démontrerez par récurrence.
En appliquant la relation à
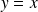, on obtient :
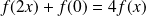, donc
.
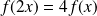Et :
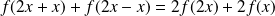, donc :
.
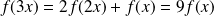On conjecture que :
.
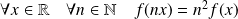On fixe
et on le démontre par récurrence double sur
.
Initialisation : La propriété est vérifiée pour
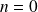et
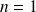(et même pour
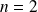et
).
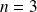Hérédité : Soit
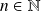tel que
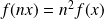et
.
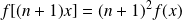D'après la relation vérifiée par
:
.
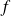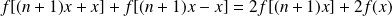Donc :
.
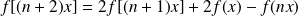Donc :
.
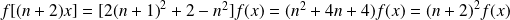Conclusion :
.
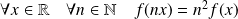Question
On pose
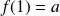. Pour tout réel
, déterminer
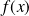en fonction de
et de
.
Déterminez
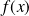en fonction de
et de
successivement pour
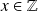, puis pour
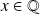, puis pour
.
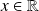D'après ce qui précède, si
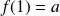, alors :
.
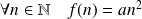Et par parité :
.
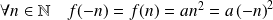Donc :
.
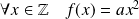Tout rationnel x peut s'écrire
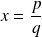avec
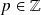et
.
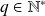Donc :
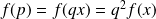. Donc :
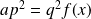. Donc :
.
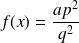Donc :
.
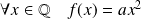Tout réel
est limite d'une suite
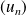de rationnels, par exemple :
.
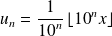Donc par continuité de
:
.
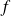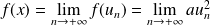Conclusion :
.
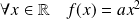Question
En déduire l'ensemble
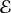des fonctions continues sur
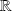, qui vérifient :
.
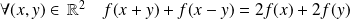Examinez si toutes les fonctions trouvées appartiennent à
.
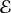On vient de montrer que
.
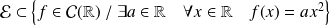Réciproquement, soit
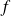une fonction de la forme :
.
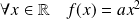Elle est continue sur
.
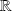Et :
.
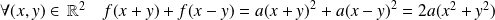Donc :
.
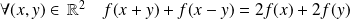Donc la fonction
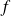appartient à l'ensemble
.
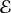Donc :
.
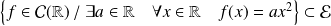Conclusion : L'ensemble
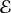est l'ensemble des fonctions de la forme
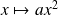où
.
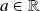