Exo 4
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
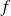la fonction définie par :
.
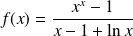Question
Etudier la continuité de la fonction
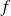sur son ensemble de définition.
Utilisez les opérations sur les fonctions continues.
Le dénominateur
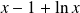s'annule si et seulement si
.
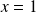Donc la fonction
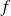est définie sur
.
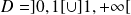La fonction
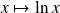est continue sur
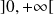et la fonction
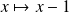est continue sur
.
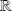Donc par addition, la fonction
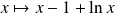est continue sur
.
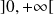Par produit, la fonction
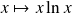est continue sur
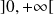et la fonction
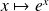est continue sur
.
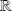Donc, par composition, la fonction
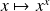est continue sur
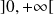car :
.
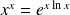Donc, par addition, la fonction
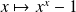est continue sur
.
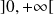Et le dénominateur
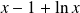s'annule si et seulement si
.
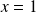Donc, par quotient, la fonction
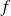est continue sur
.
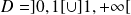Conclusion : La fonction
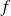est continue sur son ensemble de définition
.
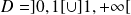Question
La fonction
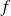est-elle prolongeable par continuité aux bornes de son ensemble de définition ?
Déterminez les limites de
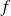en
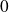et en
.
On cherche la limite de la fonction
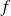en
.
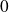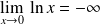donc :
.
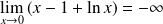Et :
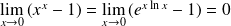car
.
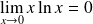Donc :
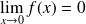. Donc
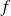admet en
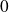une limite finie.
Conclusion : La fonction
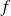est prolongeable par continuité en
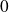en posant
.
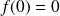On cherche la limite de la fonction
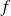en
.
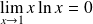et
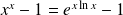. Donc :
.
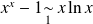Donc :
.
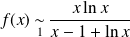Or :
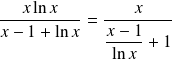et :
.
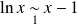Donc :
.
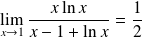Donc :
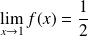. Donc
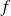admet en
une limite finie.
Conclusion : La fonction
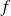est prolongeable par continuité en
en posant
.
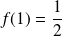