Exo 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
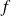une fonction continue sur
.
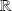Question
Démontrer que, si
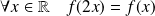, alors la fonction
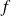est constante.
Utilisez la suite de terme général
.
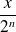La condition
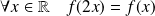peut aussi s'écrire :
.
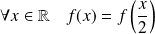Donc une récurrence évidente montre que :
.
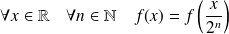Or :
.
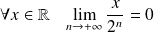Donc par continuité de
en
:
.
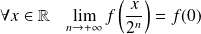Donc par unicité de la limite :
.
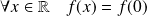Conclusion : La fonction
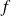est constante.
Remarque :
On peut remarquer qu'il suffit que la fonction
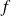soit continue en
.
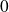Question
Démontrer que, si
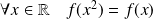, alors la fonction
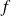est constante.
Utilisez la suite de terme général
.
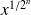On peut remarquer que :
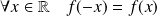puisque
.
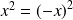On limite donc l'étude à
.
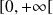La condition
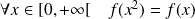peut aussi s'écrire :
.
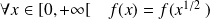Une récurrence évidente montre que :
.
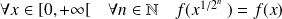Or :
.
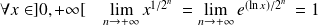Donc par continuité de
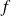en
:
.
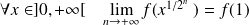Donc par unicité de la limite :
.
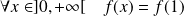Et par continuité de
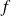en
:
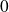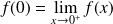. Donc :
.
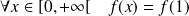Et par parité :
.
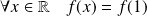Conclusion : La fonction
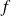est constante.
Remarque :
On peut remarquer qu'il suffit que la fonction
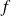soit continue en
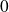et en
.
