Exo 13
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
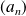une suite de réels strictement positifs.
On définit la suite
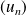par :
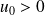et :
.
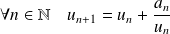Question
Montrer que la suite
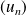converge si et seulement si la série
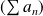est convergente.
Etudiez le sens de variations de la suite
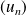, puis démontrez successivement les deux implications.
Une récurrence évidente montre que :
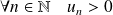, et donc :
.
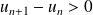Donc la suite
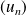est bien définie, et elle est positive et croissante.
On démontre successivement les deux implications.
On suppose que la suite
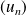est convergente. Soit :
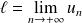.La suite est croissante, donc :
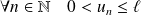, donc
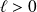et :
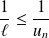, donc :
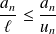.Donc :
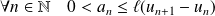. Or la série
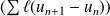est convergente car
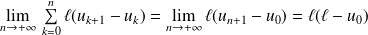. Donc la série
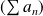est convergente.
On suppose que la série
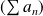est convergente. Soit :
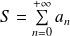.La suite
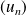est croissante, donc :
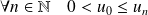, donc :
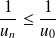.Donc :
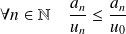. Donc :
.
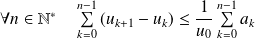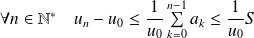, donc
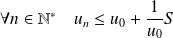.Donc la suite
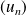est croissante et majorée, donc convergente.
Conclusion : La suite
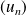est convergente si et seulement si la série
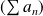est convergente.
