Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
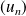 la suite définie par :
la suite définie par :
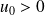 et :
et :
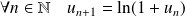 .
.
Question
Etudier la convergence de la suite
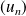 .
.
Montrez l'existence de
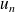 et étudiez le sens de variations de la suite.
et étudiez le sens de variations de la suite.
Une récurrence évidente montre que :
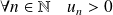 car
car
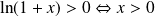 .
.
Donc la suite est bien définie.
La fonction
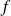 :
:
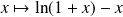 est continue et strictement décroissante sur
est continue et strictement décroissante sur
 car
car
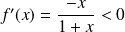 si
si
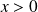 .
.
Donc
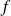 définit une bijection de
définit une bijection de
 dans
dans
 .
.
Donc :
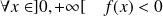 et
et
 .
.
Donc :
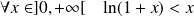 . Donc :
. Donc :
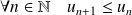 .
.
Donc la suite
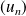 est décroissante et minorée par
est décroissante et minorée par
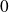 . Donc elle converge.
. Donc elle converge.
Comme la fonction
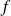 est continue sur
est continue sur
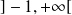 , la limite de
, la limite de
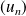 est solution de l'équation
est solution de l'équation
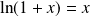 , donc de
, donc de
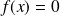 et elle est positive ou nulle.
et elle est positive ou nulle.
Conclusion : La suite
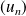 converge vers
converge vers
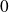 .
.
Question
Etudier la convergence de la série de terme général
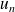 .
.
Etudiez la convergence de la suite
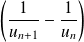 en utilisant un développement limité.
en utilisant un développement limité.
La condition nécessaire de convergence d'une série est vérifiée puisque :
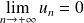 .
.
De plus :
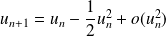 par développement limité du logarithme.
par développement limité du logarithme.
Donc :
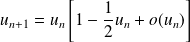 . Donc :
. Donc :
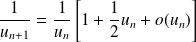 .
.
Donc :
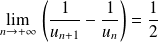 . Donc, d'après le théorème de Césaro :
. Donc, d'après le théorème de Césaro :
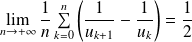 .
.
Donc :
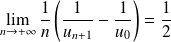 . Donc :
. Donc :
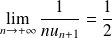 . Donc :
. Donc :
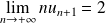 .
.
Donc
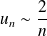 . Donc la série à termes positifs
. Donc la série à termes positifs
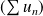 est de même nature que la série
est de même nature que la série
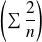 .
.
Or la dérie
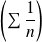 est une série de Riemann divergente (
est une série de Riemann divergente (
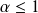 ).
).
Conclusion : La série
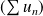 est divergente.
est divergente.





