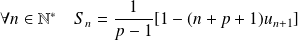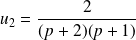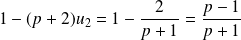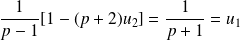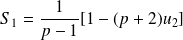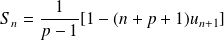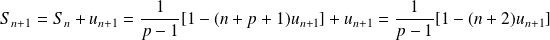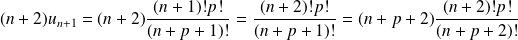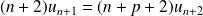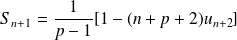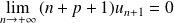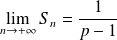Exo 12
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On rappelle la notation :
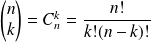 .
.
Soit
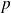 un entier naturel fixé.
un entier naturel fixé.
Pour tout
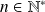 , on pose
, on pose
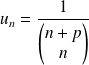 et
et
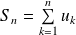 .
.
Question
Déterminer pour quelles valeurs de
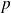 la série
la série
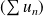 converge.
converge.
Indice
Déterminez un équivalent de
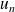 .
.
Solution
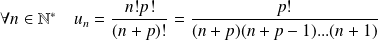 . Donc :
. Donc :
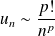 .
.
Donc la série à termes positifs
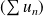 est de même nature que la série
est de même nature que la série
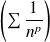 qui est une série de Riemann divergente si
qui est une série de Riemann divergente si
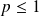 et convergente si
et convergente si
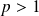 .
.
Conclusion : La série
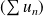 converge si et seulement si
converge si et seulement si
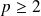 .
.
Remarque : Pour
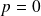 , la série diverge grossièrement car
, la série diverge grossièrement car
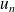 ne tend pas vers
ne tend pas vers
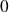 .
.