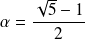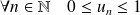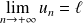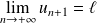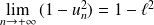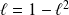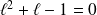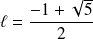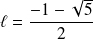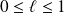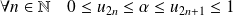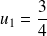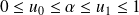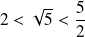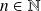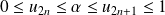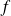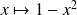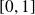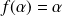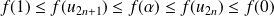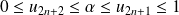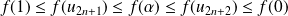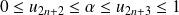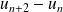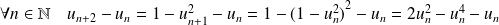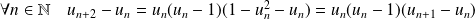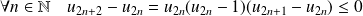Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
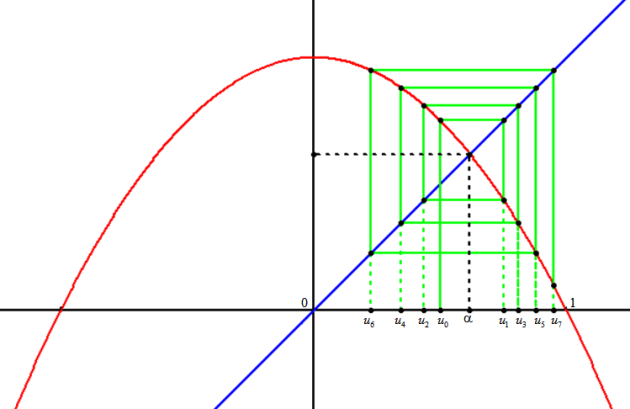
On considère la suite définie par son premier terme
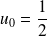 et par :
et par :
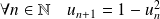 .
.
Question
Question
Question
Question
En déduire que les suites
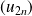 et
et
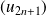 convergent mais que la suite
convergent mais que la suite
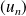 diverge.
diverge.
Si une suite converge, toute suite extraite converge vers la même limite.
La suite
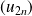 est décroissante et minorée par
est décroissante et minorée par
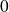 , donc elle est convergente.
, donc elle est convergente.
La suite
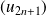 est croissante et majorée par
est croissante et majorée par
 , donc elle est convergente.
, donc elle est convergente.
Mais :
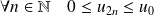 , donc :
, donc :
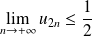 , donc :
, donc :
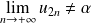 .
.
Et :
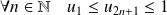 , donc :
, donc :
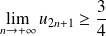 , donc :
, donc :
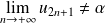 .
.
Or si la suite
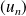 convergeait, les suites
convergeait, les suites
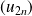 et
et
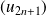 convergeraient vers la même limite, donc vers
convergeraient vers la même limite, donc vers
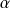 .
.
Conclusion : Les suites
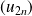 et
et
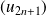 convergent mais la suite
convergent mais la suite
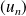 diverge.
diverge.
En fait, la suite
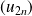 converge vers
converge vers
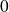 et la suite
et la suite
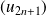 converge vers
converge vers
 .
.
Les deux suites sont monotones de sens contraires, mais ne sont pas adjacentes.