Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
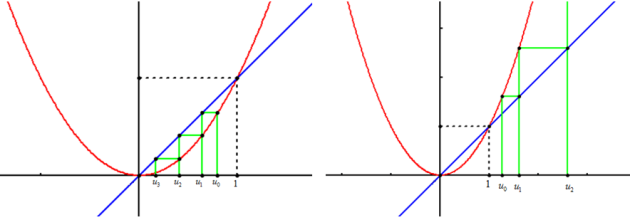
On considère la suite définie par son premier terme
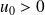 et par :
et par :
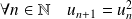 .
.
Question
Etudier le sens de variations de la suite suivant les valeurs de
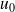 .
.
Démontrez que le sens de variations de la suite dépend de la position de
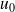 par rapport à
par rapport à
 .
.
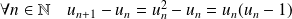 .
.
Donc le sens de variations de la suite dépend de la position de
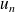 par rapport à
par rapport à
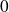 et
et
 .
.
Une récurrence évidente montre que :
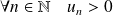 .
.
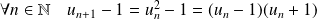 , donc
, donc
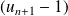 est du signe de
est du signe de
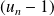 .
.
Donc, pour tout entier
 , le signe de
, le signe de
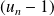 est constant : c'est le signe de
est constant : c'est le signe de
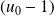 .
.
Si
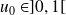 , alors :
, alors :
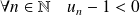 , donc :
, donc :
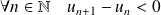 .
.
Si
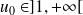 , alors :
, alors :
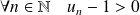 , donc :
, donc :
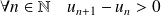 .
.
Si
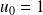 , alors :
, alors :
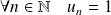 .
.
Conclusion :
Si
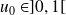 , la suite est décroissante.
, la suite est décroissante.Si
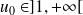 , la suite est croissante.
, la suite est croissante.Si
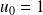 , la suite est stationnaire.
, la suite est stationnaire.
Question
En déduire l'étude de la convergence de la suite suivant les valeurs de
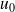 .
.
Commencez par déterminer les seules valeurs possibles de la limite de la suite.
Si la suite
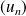 est convergente, notons
est convergente, notons
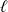 sa limite.
sa limite.
Donc :
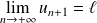 et
et
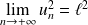 , donc par unicité de la limite :
, donc par unicité de la limite :
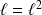 .
.
Donc, si la suite converge, sa limite est
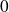 ou
ou
 .
.
Si
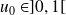 , la suite est décroissante et minorée par
, la suite est décroissante et minorée par
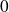 car
car
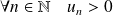 .
.
Donc, si
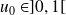 , la suite est convergente.
, la suite est convergente.
De plus :
 , donc sa limite vérifie :
, donc sa limite vérifie :
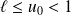 . Donc :
. Donc :
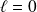 .
.
Si
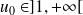 , la suite est croissante. Donc :
, la suite est croissante. Donc :
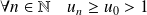 .
.
Si la suite
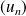 était majorée, elle serait convergente et sa limite vérifierait
était majorée, elle serait convergente et sa limite vérifierait
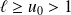 , ce qui n'est pas possible.
, ce qui n'est pas possible.
Donc, si
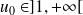 , la suite est croissante non majorée, donc elle diverge vers
, la suite est croissante non majorée, donc elle diverge vers
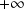 .
.
Conclusion :
Si
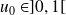 , alors la suite
, alors la suite
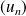 converge vers
converge vers
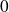 .
.Si
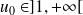 , la suite
, la suite
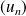 diverge vers
diverge vers
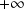 .
.Si
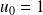 , la suite est stationnaire.
, la suite est stationnaire.