Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
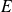 un espace vectoriel euclidien de dimension
un espace vectoriel euclidien de dimension
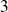 .
.
Question
Démontrer que :
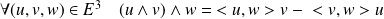 .
.
Lorsque les vecteurs
 et
et
 ne sont pas colinéaires, construisez une base orthonormée directe bien adaptée et raisonnez sur les coordonnées.
ne sont pas colinéaires, construisez une base orthonormée directe bien adaptée et raisonnez sur les coordonnées.
Si
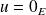 ou
ou
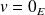 , l'égalité est vérifiée car les deux membres sont nuls.
, l'égalité est vérifiée car les deux membres sont nuls.
Si les vecteurs
 et
et
 sont colinéaires et non nuls, il existe un réel
sont colinéaires et non nuls, il existe un réel
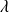 tel que
tel que
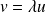 .
.Donc :
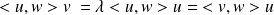 et
et
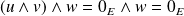 .
.Donc l'égalité est vérifiée.
Si les vecteurs
 et
et
 ne sont pas colinéaires, alors
ne sont pas colinéaires, alors
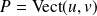 est un plan.
est un plan.Le vecteur
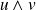 est orthogonal au plan
est orthogonal au plan
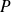 , donc il oriente
, donc il oriente
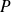 . Soit
. Soit
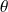 une mesure de l'angle orienté
une mesure de l'angle orienté
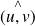 .
.On définit les vecteurs :
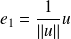 ,
,
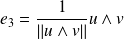 et
et
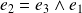 .
.On construit ainsi une base orthonormée directe
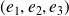 .
.Dans cette base :
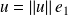 ,
,
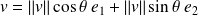 et
et
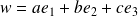 .
.Donc :
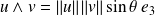 et
et
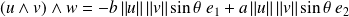 .
.Or :
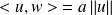 et
et
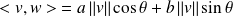 .
.Donc :
 .
.
Conclusion :
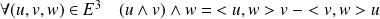 .
.
Cette formule est connue sous le nom de « formule du double produit vectoriel ».





