Orientation d'un plan dans l'espace de dimension 3
On suppose l'espace vectoriel euclidien
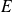 orienté et rapporté à une base
orienté et rapporté à une base
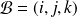 orthonormale directe.
orthonormale directe.
Définition :
Le produit mixte de trois vecteurs
 ,
,
 et
et
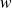 est :
est :
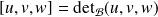 .
.
Il est indépendant de la base orthonormale directe
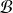 choisie.
choisie.
Fondamental :
Propriétés :
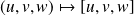 est une forme trilinéaire alternée.
est une forme trilinéaire alternée.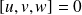 si et seulement si
si et seulement si
 ,
,
 et
et
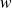 sont coplanaires.
sont coplanaires.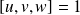 si et seulement si
si et seulement si
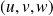 est une base orthonormale directe.
est une base orthonormale directe.
Définition :
Le produit vectoriel de deux vecteurs
 et
et
 est l'unique vecteur
est l'unique vecteur
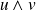 tel que :
tel que :
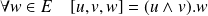 .
.
Fondamental :
Propriétés :
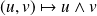 est une application bilinéaire antisymétrique :
est une application bilinéaire antisymétrique :
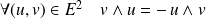 .
.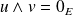 si et seulement si
si et seulement si
 et
et
 sont colinéaires.
sont colinéaires.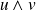 est orthogonal à
est orthogonal à
 et à
et à
 .
. Si
 et
et
 sont orthogonaux et unitaires,
sont orthogonaux et unitaires,
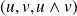 est une base orthonormale directe.
est une base orthonormale directe.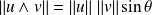 où
où
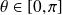 est une mesure de l'angle géométrique de
est une mesure de l'angle géométrique de
 et
et
 .
.Si
 et
et
 ont respectivement pour coordonnées
ont respectivement pour coordonnées
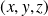 et
et
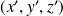 dans une base orthonormale directe, alors
dans une base orthonormale directe, alors
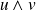 a pour coordonnées :
a pour coordonnées :
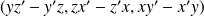 .
.
Fondamental :
Orientation d'un plan dans l'espace
Un plan
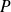 est orienté par le choix d'une base orthonormale
est orienté par le choix d'une base orthonormale
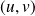 . La droite
. La droite
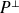 est orientée par le choix d'un vecteur unitaire
est orientée par le choix d'un vecteur unitaire
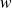 . On dira que les deux orientations sont compatibles si la base orthonormale
. On dira que les deux orientations sont compatibles si la base orthonormale
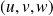 est directe.
est directe.
Si
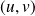 est une base orthonormale d'un plan
est une base orthonormale d'un plan
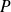 , alors
, alors
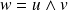 est l'unique vecteur de
est l'unique vecteur de
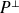 tel que
tel que
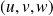 soit une base orthonormale directe.
soit une base orthonormale directe.
Inversement, si
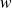 est un vecteur unitaire de la droite
est un vecteur unitaire de la droite
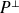 , il existe une unique orientation du plan
, il existe une unique orientation du plan
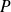 qui soit compatible avec celle de
qui soit compatible avec celle de
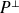 . On dira que le vecteur
. On dira que le vecteur
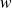 oriente le plan
oriente le plan
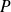 .
.





