Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère l'espace vectoriel
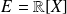des polynômes à coefficients réels.
Question
Justifier la convergence de l'intégrale
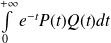pour tous les polynômes
et
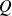de
.
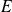Montrez que la fonction
est dominée en
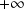par une fonction dont l'intégrale est convergente.
Pour tous polynômes
et
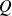, le produit
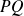est un polynôme, donc une somme de termes de la forme
.
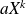Il suffit donc de justifier la convergence de l'intégrale
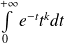pour tout entier naturel
.
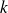La fonction
est continue sur
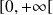et
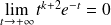, donc
.
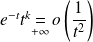Or l'intégrale
est convergente et les fonctions sont positives.
Donc l'intégrale
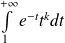est convergente.
Donc l'intégrale
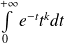est convergente pour tout entier naturel
.
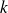Conclusion : L'intégrale
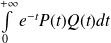est convergente pour tous les polynômes
et
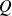de
.
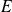Question
Montrer que l'application
:
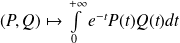définit un produit scalaire sur
.
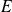Démontrez successivement les quatre axiomes en commençant par la symétrie.
L'application
:
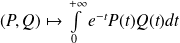est une application de
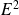dans
.
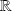Pour tous
:
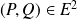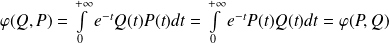.Donc la forme
est symétrique.
Montrons la bilinéarité.
Pour tous
et tout réel
:
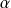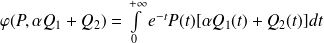.Les intégrales sont convergentes, donc :
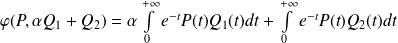.Donc :
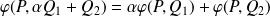.Donc, pour tout
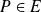, l'application
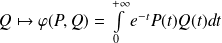est linéaire.Donc, en utilisant la symétrie, la forme
est bilinéaire.
Montrons que la forme
est définie et positive.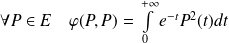
, donc
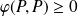car
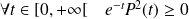.La fonction
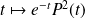est continue et garde un signe constant sur
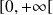. Donc l'intégrale est nulle si et seulement si la fonction est nulle.
Donc
si et seulement si
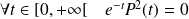. Or
.Donc
si et seulement si
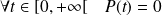, donc si
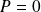.Donc la forme
est définie et positive.
Conclusion : L'application
:
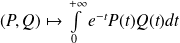définit un produit scalaire sur
.
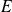