Exo 1
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Rappel : L'ensemble
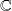des nombres complexes est un
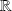- espace vectoriel.
Question
Démontrer que l'application
:
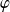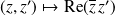définit un produit scalaire sur
.
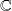Démontrez successivement les quatre axiomes en commençant par la symétrie.
L'application
:
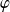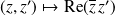est une application de
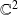dans
.
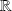Montrons la symétrie.
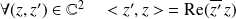. Or :
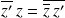.Et deux nombres complexes conjugués ont la même partie réelle.
Donc :
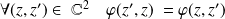. Donc la forme
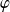est symétrique.
Montrons la bilinéarité.
Par distributivité de la multiplication par rapport à l'addition, l'application
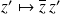est linéaire pour tout
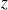. Et l'application
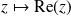est linéaire.Donc, pour tout
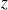, l'application
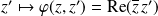est linéaire.Donc, en utilisant la symétrie, la forme
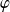est bilinéaire.
Montrons que la forme
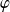est définie et positive.
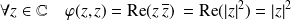. Donc :
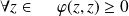.Et
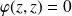équivaut à
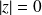, donc à
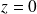.Donc la forme
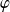est définie et positive.
Conclusion : L'application
:
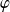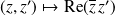définit un produit scalaire sur
.
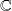Remarque :
Si l'on considère les formes algébriques
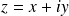et
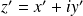, alors :
.
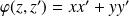On retrouve l'expression du produit scalaire usuel sur
.
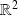