Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
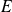un espace vectoriel de dimension
.
Question
Montrer que si
et
sont deux formes linéaires non nulles sur
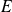qui ont le même noyau, alors, il existe
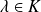tel que
.
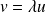Introduisez un supplémentaire de leur noyau.
et
sont deux formes linéaires non nulles.
Donc leur noyau
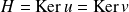est un hyperplan de
.
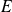Un supplémentaire
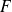de
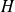est donc de dimension
. Soit
une base de
.
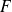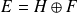. Donc :
.
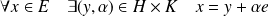Donc :
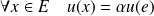et
.
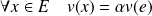Or
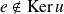. Donc
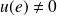et donc :
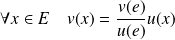. Donc :
.
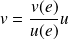Conclusion : Il existe
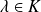tel que
.
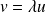Soit
une forme linéaire non nulle sur
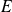de noyau
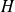, et
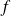un endomorphisme de
.
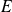Question
Montrer que
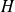est stable par
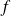si et seulement si il existe
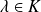tel que :
.
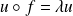Raisonnez par double implication.
Et comparez les noyaux des formes linéaires
et de
.
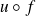Si
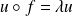, alors :
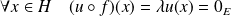, donc
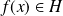. Donc
.
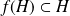Donc si
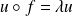, alors l'hyperplan
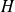est stable par
.
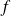Réciproquement, supposons que l'hyperplan
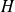soit stable par
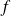. Donc :
.
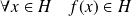Donc :
.
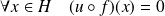Donc il y a deux cas :
soit la forme linéaire
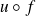est nulle, et donc
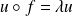avec
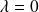.soit la forme linéaire
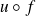n'est pas nulle, et donc son noyau est un hyperplan qui contient
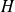, donc son noyau est
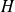. Donc les formes linéaires
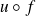et
ont le même noyau. Donc il existe
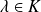tel que
.
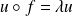Conclusion : L'hyperplan
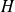est stable par
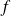si et seulement si il existe
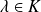tel que :
.
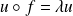Question
Application : Déterminer les plans stables par l'endomorphisme
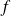de
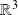de matrice
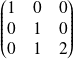dans la base canonique.
Trouvez les noyaux des formes linéaires
non nulles telles que
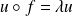où
.
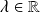Il suffit de trouver toutes les formes linéaires
non nulles telles que
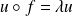où
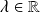, puis de déterminer leurs noyaux.
Soit
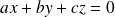(avec
,
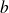et
non tous nuls) une équation de
.
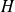Donc
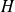est noyau de la forme linéaire
:
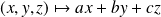de matrice
.
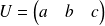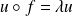équivaut à
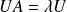, donc à :
.
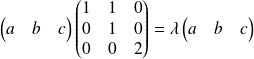Donc :
.
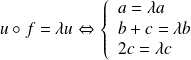Si
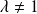et
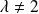, alors
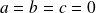, ce qui est contraire à l'hypothèse.
Si
,
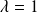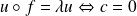. On obtient tous les plans d'équation
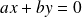avec
.
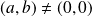Si
,
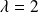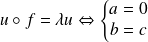. On obtient le plan d'équation
.
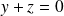Conclusion : Les plans stables par l'endomorphisme
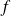sont les plans d'équations
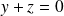ou
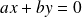avec
.
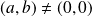Complément : Complément
Une forme linéaire non nulle a pour matrice une matrice ligne
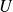non nulle.
Donc :
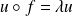équivaut à
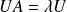, donc à
.
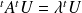Donc
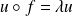si et seulement si
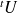est vecteur propre de la matrice
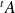associé à la valeur propre
.
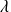Pour déterminer les hyperplans stables par
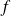, on est donc ramené à déterminer les vecteurs propres de la matrice
.
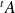