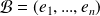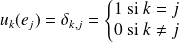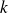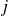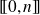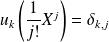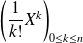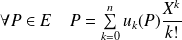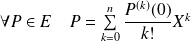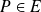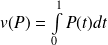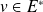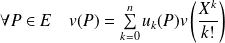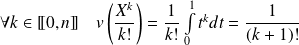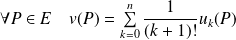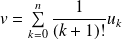Exo 1
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Dans l'espace vectoriel
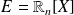, on définit, pour tout
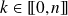, l'application
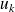qui à tout polynôme
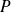associe
.
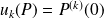Question
Montrer que
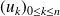est une base du dual
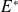de
.
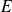Pour montrer l'indépendance, utilisez la base canonique de
.
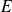Par linéarité de la dérivation, pour tout
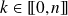, l'application
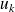est une forme linéaire sur
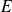, donc appartient à
.
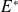Montrons que la famille
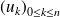est libre. Soit
,
, ...,
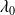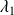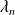des réels.
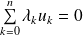si et seulement si :
.
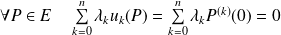Donc en particulier, pour la base
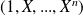de
:
.
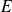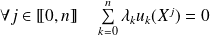Or, pour tout
:
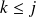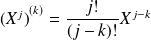. Et pour tout
:
.
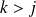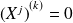Donc :
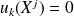pour tout
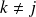. Et
.
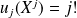Donc :
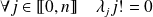. Donc :
.
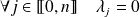Donc la famille
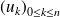est une famille libre de
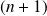vecteurs dans l'espace vectoriel
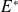qui est de même dimension que
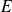, donc de dimension
.
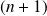Conclusion : La famille
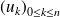est une base de
.
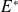