Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Montrer que les matrices
,
,
et
forment une base
de
.
Il suffit de démontrer que la famille est libre.
Montrons que la famille
est libre.
Soit
tel que :
.
Donc :
.
Donc :
.
En additionnant les lignes, on obtient
.
Donc :
. Donc la famille
est libre.
C'est une famille libre de
vecteurs dans l'espace vectoriel
qui est de dimension
.
Conclusion : La famille
est une base de
.
Question
Déterminer les coordonnées d'une matrice
dans la base
.
si et seulement si :
.
En additionnant les lignes, on obtient :
.
Conclusion : Les coordonnées de
dans la base
sont
.
Question
Soit la matrice
et
l'endomorphisme de
qui à toute matrice
de
associe la matrice
.
Déterminer la matrice de
dans la base
de
.
Exprimez les images des vecteurs de la base
de
dans la base
.
La linéarité de
a été démontrée dans l'exercice
.
.
Donc
d'après la deuxième question.
.
Donc :
d'après la deuxième question.
Donc :
d'après la deuxième question.
.
Donc :
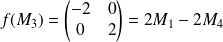d'après la deuxième question.
Conclusion : La matrice de
dans la base
est
.
