Matrice d'une application linéaire
Tous les espaces vectoriels considérés sont de dimension finie.
Définition :
Soient
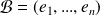 une base de
une base de
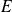 et
et
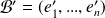 une base de
une base de
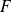 .
.
La matrice d'une application linéaire
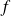 de
de
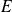 dans
dans
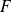 est la matrice
est la matrice
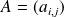 définie par :
définie par :
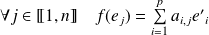 .
.
La matrice dépend évidemment des bases
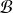 et
et
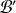 .
.
Fondamental :
Si
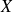 est la matrice colonne des coordonnées d'un vecteur
est la matrice colonne des coordonnées d'un vecteur
 de
de
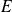 dans la base
dans la base
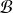 , le vecteur
, le vecteur
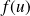 a pour matrice
a pour matrice
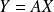 dans la base
dans la base
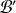 .
.
Fondamental :
Opérations
Soient
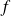 et
et
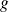 deux applications linéaires de matrices
deux applications linéaires de matrices
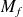 et
et
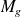 . Sous réserve d'existence :
. Sous réserve d'existence :
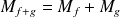 .
.  .
. 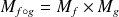 .
.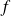 est bijective si et seulement si
est bijective si et seulement si
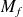 est inversible et
est inversible et
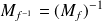 .
.
Fondamental :
Changement de base
Soit
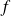 un endomorphisme de
un endomorphisme de
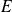 .
.
Si
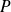 est la matrice de passage d'une base
est la matrice de passage d'une base
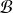 de
de
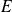 à une base
à une base
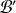 de
de
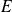 , les matrices
, les matrices
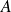 de
de
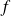 dans
dans
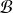 et
et
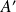 de
de
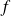 dans
dans
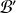 vérifient :
vérifient :
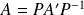 .
.
Les matrices
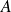 et
et
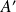 sont dites semblables.
sont dites semblables.
Alors :
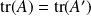 ,
,
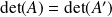 et
et
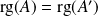 .
.
Définition :
On définit donc :
la trace d'un endomorphisme :
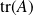 où
où
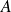 est la matrice de
est la matrice de
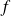 dans une base quelconque.
dans une base quelconque.le déterminant d'un endomorphisme
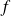 :
:
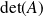 où
où
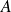 est la matrice de
est la matrice de
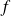 dans une base quelconque.
dans une base quelconque.le rang d'un endomorphisme :
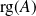 où
où
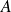 est la matrice de
est la matrice de
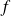 dans une base quelconque.
dans une base quelconque.





